Sorry! See you in class.
Month: October 2019 (Page 1 of 2)
Hi everyone,
Your Midsemester Grades (including your grades for Exam #2) are posted on the OpenLab Gradebook (Dashboard / OpenLab Gradebook). You will see that your grades for Exam #2 as well as your current Homework, OpenLab, and Project grades have been posted.
Your Midsemester grade is based on the following work completed so far:
Homework 30%, OpenLab 25%, Exams 45%
Midterm grade key:P: passing/satisfactory progress; likely to complete course requirements.U: failing/unsatisfactory progress; not likely to complete course requirements.BL: borderline; barely passing or just below passing; there is a reasonable expectation that the student will pass the courseSA: stopped attending; for students who were attending (at least once) and have now have stopped attending your class.WN grade: Student never attended. Do not assign this grade. This information was based on the “ verification of attendance” (VOA) roster you submitted at the 3rd week of the semester.
Let me know if you have any questions.
Regards,
Prof. Reitz
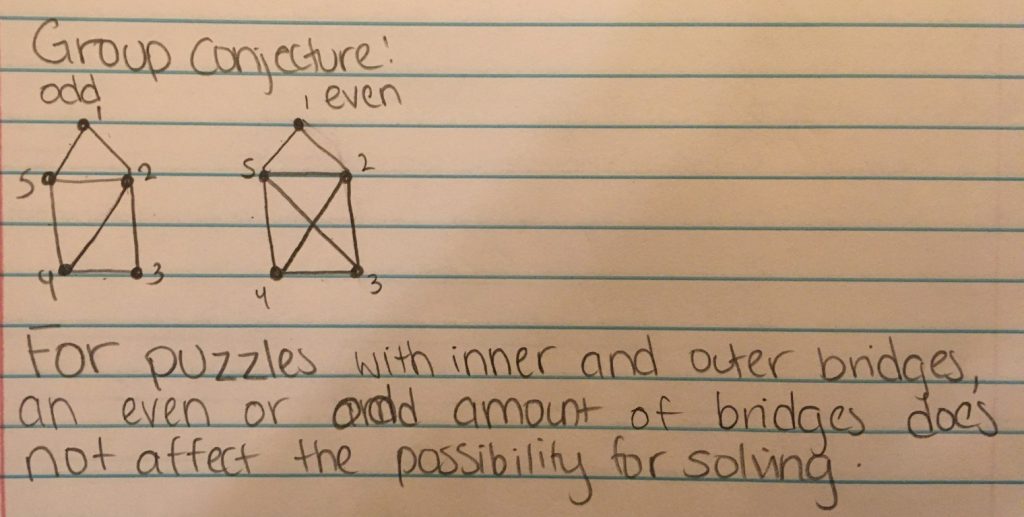
Your assignment for the coming week+ is to try to prove the conjecture that your group created in class on Thursday, 10/24. You may need to refine/expand your conjecture first (let’s discuss this in class). You must spend at least 90 minutes working on this. Trying to prove something can consist of many different activities, such as the following (you do NOT have to do all of these things – you can choose how to spend your time – they are provided for inspiration only).
- coming up with ideas, and testing them out (for example, by creating puzzles and trying to solve them)
- trying to understand what the conjecture says
- trying to solve puzzles that other people created
- trying to create puzzles (and solve them yourself)
- communicating with other members of your group (talking, emailing, etc.)
- trying to write down a proof
- other stuff…
As you work, keep track of what you are doing, thinking, and feeling (this is metacognition – an idea that discussed way back in OpenLab #2). What did you do during the time you spent? Did you create any puzzles? Did you solve puzzles? Did you change your mind about whether the conjecture is true or false? Did you have any new ideas about how to prove the conjecture? Did you have any ideas that you gave up on? How did you feel as you worked – were you frustrated/confused/happy/depressed? Why? Did your mood change along the way?
Assignment (Due Thursday, 11/7): Submit a journal of your efforts in the comments below. Your response should be at least 300 words. Describe what you did during the 90 minutes you worked, and express in some way what you were thinking and feeling during the process. Your response can include puzzles (use sketchtoy.com) or other work you did along the way.
Extra Credit. Respond to a fellow student’s comment. Did you do similar things? Different things? Do you have any suggestions for them? Be kind.
GROUP CONJECTURES (created in class 10/24):
Group 1: Song Yu, Randy, Aurkaw
Group 2: Youshmanie, Dylan
Written work, Due Tuesday, November 5th, in class:
From last week: Chapter 4: 27, 28, Chapter 5: 29, 31
Chapter 6 p.116: 3, 4, 5, 8, 9
WeBWorK – none
OpenLab – OpenLab #6 due Thursday, November 7th
NOTE: As a component of OpenLab #5, each person should bring to class a conjecture or question about the Bridges and Walking Tours game.
Group Activity (30 min). Get into your groups, arrange your chairs in a circle, and take 30 minutes to complete the following:
1. Each person should share their conjecture with the group. For each conjecture, the group should decide if they think it is true or false (or don’t know). The group should record their conclusion for each conjecture.
2. Choose one conjecture (or create a new one) to focus on as a group. Your goal for the next few weeks will be to try to prove or disprove this conjecture. Come up with several ideas about how you might prove it.
Group work due after 30 minutes: Each group will hand in a sheet of paper with the names of the group members, the date, and the following:
– Each member’s conjecture, along with a brief description of what the group thinks – is it true or false?
– Be sure to clearly indicate which of the conjectures the group has chosen to work on – or, if you have created a new conjecture to work on as a group, include that as well.
– Two different ideas about how you might try to prove the chosen conjecture.
Reflection: To be completed individually after group work is complete, and submitted on paper with your names and the date. Take 5 minutes to write on the following prompt:
Briefly reflect on the process of working in a group by responding to each of these points:
1. Describe something you learned.
2. Describe something you contributed to the group.
3. How did today’s work change your understanding of the “bridges and walking tours” game?
Written work, Due Tuesday, October 29, in class: Chapter 5: 1, 4, 9
GCD Problems: Because of the exam, these problems will not be due until Tuesday, November 5:
Chapter 4 p.101: 27, 28
Chapter 5 p.110: 29, 31
WeBWorK – none
OpenLab – none
Written work, Due Tuesday, October 22, in class:
Chapter 4 p.100: 4, 5, 10, 11
Odd problems are worth 4 points, even problems worth 8 points.
WeBWorK – none
OpenLab – Recall: OpenLab #5 due at the beginning of class on Thursday, 10/24. NOTE: Please complete the writing portion on the OpenLab, but bring your Conjecture to class on 10/24 (do not post your Conjecture to the OpenLab)
In 2002, a mathematician named Paul Lockhart wrote an essay called “A Mathematician’s Lament,” a passionate criticism of mathematics education in America. It has become widely known among mathematicians and mathematics educators – not everyone agrees with everything he says (though many do), but everyone seems to have something to say about “Lockhart’s Lament,” as it is called. For this week’s assignment, you will read a short excerpt (three pages) from his essay and respond to the prompts below.
Assignment (Due Thursday, 10/24/17). Your assignment has three parts:
First, read the section titled “Mathematics and Culture” (pages 3-5) in Lockhart’s essay, (click here). If you’re interested, I encourage you to read more, starting at the beginning – but this is not required.
Second, write a response to what you read and post it in the comments below. Your response should be at least 300 words. Your response should represent your own thoughts and opinions on what you read, and can include responses to any or all of the following:
- What is one thing that you agree with in the reading? Explain why.
- What is one thing that you do not agree with? Explain.
- Choose one quote that you think stands out in the reading. Give the quote, and explain why you chose it.
- Have you ever had an experience of mathematics as art?
- On page 5, Lockhart describes mathematics in schools today as “heartbreaking”. What do you think he means? Do you agree? How do your own math experiences in school compare to his description?
Third, and most important, I want you to write down a conjecture about the Bridges and Walking Tours game, and bring it with you to class on Thursday 10/24 (do NOT post it here). Consider Lockhart’s example of a triangle drawn inside a rectangle. He described the process of playing around with this picture, until he arrives at the basic idea for calculating the area of a triangle. He contrasts this with a traditional math class, in which the formula is given to students without providing them any opportunity to explore the problem on their own. The bridges and walking tours game is a little like the triangle-rectangle picture – it’s fun to play around with, but you may not be sure what the point is. You’ve had a chance to play with it a bit, and try some different challenges. Now what? Your job is write down a conjecture (a guess!) or a question about your game. Write down a conjecture or question about the bridges and walking tours game, and bring it with you to class on Thursday 10/24 (do NOT post it here).
Here is an example: Let’s imagine that you have just been introduced to the game Tic-Tac-Toe. After playing it for a while, you might come up with one of the following conjectures about Tic-Tac-Toe:
Conjecture: The person who goes first always wins.
Conjecture: The center is the best move.
Conjecture: It’s impossible to win, no matter who goes first.
ps. Paul Lockhart retired from being a first-rate research mathematician in order to teach math at a private elementary school here in Brooklyn, Saint Ann’s School, where he says “I have happily been subversively teaching mathematics (the real thing) since 2000.”
Group Activity (25 min). Get into your groups (group assignments appear below), arrange your chairs in a circle, and take 25 minutes to:
1. Share your responses to OpenLab #4. Compare your answers to the given examples (do you all agree on the solutions?). Now share your own puzzles with the group, and discuss.
2. Create three new puzzles, as tricky as possible (try to stump Prof. Reitz!).
Group work due after 25 minutes: Each group will hand in a sheet of paper with the names of the groups members, the date, and the three new puzzles created by the group. You do not need to submit solutions, but you do need to be able to solve the puzzles on request.
Reflection: To be completed individually after group work is complete, and submitted on paper with your name and the date. Take 5 minutes to write on the following prompt:
Briefly reflect on the process of working in a group by responding to each of these points:
1. Describe something you learned.
2. Describe something you contributed to the group.
3. How did today’s work change your understanding of the bridges and walking tours game?
Group Assignments
Group 1: Song Yu, Randy, Aurkaw
Group 2: Youshmanie, Dylan
Written work, Due Thursday, October 17th, in class:
Chapter 4 p.100: 1, 6, 7, 15, 16
Odd problems are worth 4 points, even problems worth 8 points.
WeBWorK – none
OpenLab – OpenLab #5 Due Thursday 10/24. NOTE: Please complete the writing portion on the OpenLab, but bring your Conjecture to class on 10/24 (do not post your Conjecture to the OpenLab)





Recent Comments