In his essay A Mathematician’s Lament, Paul Lockhart says “A good problem is something you don’t know how to solve.” This is quite different from most of the “problems” that appear in our mathematics education. In the past weeks, you’ve all spent some time individually and in groups working on such problems, in the context of graph theory (“Bridges and Walking Tours”).
As a group, write an account of your experiences working on your puzzle/problem. You should include the following elements:
- Description of the Bridges and Walking Tours problem, in your own words.
- An account of working on your problem as a group, from playing with the problem to formulating and perhaps proving a conjecture. What did your group do/think/feel? You can include examples of puzzles and solutions if you wish, as well as work by individual group members completed outside the group (both optional). Your goal is not to go over every detail, but to tell a story that your readers will enjoy – “what was it like”?.
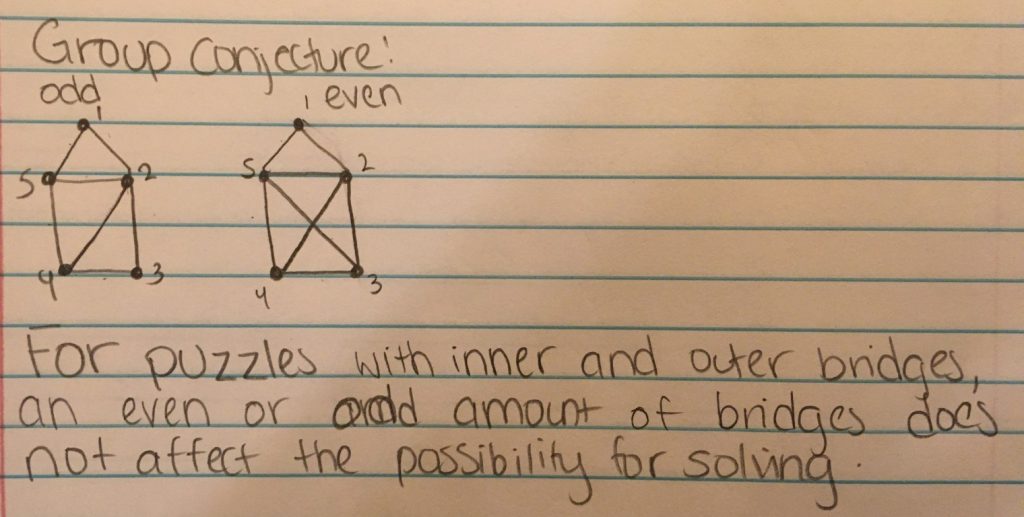
- A statement of your group’s chosen conjecture, and a proof (or disproof) of the conjecture.
- At least three images (more if you wish). They can include images of puzzles you’ve created or solutions, but you can also be creative with images or photos related to your puzzle, your group or your story in some way. Each image should have a caption describing. NOTE: You may freely use your own drawings, images or photos. If you wish to use photos from another source, they must be from a legal source (for example, Creative Commons licensed, with proper attribution – the library or your professor can help with this).
- Basic details: the names of all group members, the date, course and section numbers, and your professor’s name.
I will be meeting with each group next Tuesday, November 14th, in class. Please be in touch with your other group members before then! Be prepared to discuss your progress so far – at the very least, you should be able to describe how you are dividing up the work of the paper among your group.
The first draft of this assignment is due in class on Thursday, November 21. Each group should submit one paper, of no less than 1500 words. You may decide as a group how to divide up the work. Be aware that you will be asked at a later time to describe your own specific contributions as well as those of each group member.
The final draft of this assignment is due in class on Tuesday, December 5.
REGARDING SEMESTER PROJECT: As you may recall from the Course Description, the semester project is worth 10% of your overall grade. The project consists of a number of interrelated activities (many of which have already been completed) – complete details can be found on the Project Overview & Deliverables page. The group paper assigned here forms a significant portion of the project.
Group 1: Song Yu, Randy, Aurkaw
A diagram is solvable when a diagram has a greater than or equal to a number of vertices with an even number of adjacent lines than the number of vertices with an odd number of adjacent lines. And a line graph is solvable by choosing either of the endpoints of a line.
Group 2: Youshmanie, Dylan:
A puzzle is solvable with a bit string where the length is the total number of points and the elements are the amount of bridges connected to each point in descending order then the pattern is solvable for any other puzzle with the same bit string.





Recent Comments