The last significant group assignment for your semester project is a group presentation (there will be one more individual assignment, a reflection on the process). I’ll put the details here, followed by an outline of the grading criteria (the presentation is worth 20 points total).
Semester Project – Group Presentation
This is your chance to share your group’s work with the rest of the class. Each group will give a 5-8 minute presentation, including the following items:
- State your conjecture (this should be written down, either on a slide or on the board). Give an explanation, and an example to demonstrate your conjecture.
- If you were able to prove your conjecture, give a proof. If not, describe briefly some of the ideas you had and strategies you tried while trying to prove it.
- Give the class at least one puzzle to work on on their own – a challenge!
- Give the audience a chance to ask questions (either during the presentation, or after).
Keep in mind the following:
- You must include some kind of slides (you may also put work on the board): PowerPoint, Google Slides, Prezi.com, LaTeX Beamer, or other.
- You may decide as a group how to divide up the work, but each group member must present something to class.
- Be aware that you will be asked at a later time to describe your own specific contributions as well as those of each group member.
- Presentations will be given at the beginning of class on Tuesday, 12/5 and Thursday, 12/7. Your group must sign up for a presentation time before leaving class on 11/14.
Grading Criteria (20 points total)
_____ points (4 possible). Basics. Stay within time limits (5-8 minutes). All group members participate.
_____ points (6 possible). Conjecture. Conjecture is written down. Explanation and example are provided.
_____ points (7 possible). Proof of conjecture or proof process description.
_____ points (3 possible). Challenge the class. At least one puzzle is given for the class to work on on their own.
____ points TOTAL (20 possible)



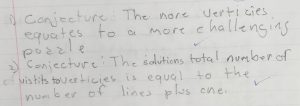





Recent Comments