Hello classmates, here are the notes from the second class. Material is from lecture, questions, lab presentation and the board.
The knot of the week was the clove hitch. A hitch is a knot that ties to something fixed. We practiced with our fingers or arms. To make the clove hitch wrap one of the rope completely around the finger/arm and over itself. Wrap a second time and have the rope go under the second wrap. Pull tightly.
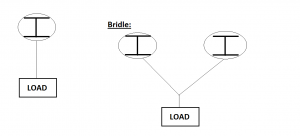
Dead hang: Something hung under a support and stays still
A rigger must notify the engineer for a building for all the bridles that will be hung in a space/arena. Certain beams and support are used for the building/space exclusively.
Can you put a motor on a bridle? No, a motor works for linear support and doesn’t do well in angle loads Correction, a motor can be on a bridle but not as one of the bridles.
What’s the difference with forces between a dead hang and a bridle? Dead Hang has only vertical forces while bridle has vertical and horizontal forces.
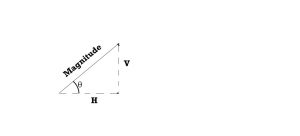
Vector:
Contains:
-Magnitude
-Direction
It’s arbitrary which axis is used to measure the angle but for class purposes we’ll use horizontal axis.
When vectors are added we end up with a new vector.
For each vector we have a vertical component & horizontal component.
Trigonometry: “If you get a cold sweat from hearing it , then don’t.”
An easy way of remembering trigonometric functions to solve for theta (angle) is to use:
SohCahToa
Sine(θ) = Opposite/Hypotenuse
Cosine(θ) = Adjacent/Hypotenuse
Tangent(θ) = Opposite/Adjacent
Note: Symbol for theta is θ. Theta is the angle.
Example:
Magnitude = 13.7 lbs
θ = 30°
Sin(30°) = Opp/137 lbs -> Sin(30°) = 0.5
0.5 = Opp/137 lbs -> 0.5 * 137lbs = Opp = 68.5 lbs
Note: Make sure your calculator is set to degree and not radiant.
We must use pythagorean theorem to solve this problem.
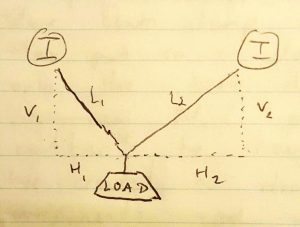
Figure 2-4
T is the tension force countering the pull by the rope in the bridle.
T₁ = (L₁ * H₂ * P (P stands for Load))/ (V₁ * H₂ + V₂ * H₁)
T₂ = (L₂ * H₁ * P)/(V₁ * H₁ + V₂ * H₁)
Vf₁ = (V₁ * H₂ * P)/(V₁ * H₂ + V₂ * H₁)
Vf₂ = (V₂ * H₁ * P)/(V₁ * H₂ + V₂ * H₁)
To check if correct:
Vf₂ + Vf₁ + P = 0
Pythagorean Triplets are the proportions that always match on a right triangle. The lowest of these are 3-4-5, with 5 always the hypotenuse.
Lab time!
New piece of hardware introduced: Beam Clamp
It has a plate that contains Max load and badge # in case of product failure and
manufacturer can then recall.
The beam clamp used had 1 ton max load. We scaled a sand bag at 49 lbs.
Max put a clove hitch with a rope and onto the beam clamp. Professor McCullough put a half clove hitch on a carabiner to hang the scale and sand bag. We created first a dead hang. It was a dead hang because all our components can withstand a 49 lbs. fource.
We took a measuring tape and with a second scale we pulled the sand bag 2 feet. Pulling the sand bag was over 30 lbs. force! This shows that pulling a 300 lbs. curtain can easily take over 100 lbs.
Figure 2-5
A pear ring can withstand forces from various angles.
We also used a munter hitch on one of our hangs.
Now scaling two sand bags on a bridle. Stage right had 40 lbs. Stage left had just under 35. We made an experimentation to shorten the stage left rope of the bridle. Only a little change increased on each rope. We then spread the beam clamps further apart and then each rope had 55 lbs. in tension. This showed that we can create higher loads than what we hung.
For the next lab exercise, we hung a 10 lbs. sand bag. Two people held the rope on each side of the rope respectively. If they both held the rope vertically over the sand bag, each person would have half the load of the sand bag. But by moving away from each other, the load kept increasing for each person. The vertical load is not changing. The θ (theta) is changing and the smaller the θ the greater the force. But it could never be straight, it would become an infinite force. It’s impossible to hang curtain over a perfectly straight cable. Even a beam sags a little bit but the sag is unnoticeable.
Stress = Actual force/Area
f₁ = Pressure/Area
F₁ = Maximum Allowable Stress
f₁ < F₁ is OK while f₁ > F₁ is NOT OK!
Strain = Deformation
ΔL/L₀ or Change in length/Original length
Types of forces:
-Compression
-Tension
-Torsion
Elastic rouge of material deforms and returns to original shape.
Ultimate Breaking Strength or UBS sometimes referred as Ultimate Strength or Breaking Strength is the capacity of the material to withstand a load.
Design Factor (DF), or Safety factor but riggers have strayed from using it because people thought it was a perfect safe system.
WLL = Working Load = UBS/DF
Riggers mostly use a design factor of 5 Throughout the semester we’ll talk about which design factors to use. Design factor should correspond to how much possible negative consequences and account possible unkoown.
New WLL = (Old WLL * Old DF)/New DF
End of notes.
-Charlie





Charlie, these notes are great. Thanks for posting. I should clarify – you can hang a motor from a bridle, but you would not usually use it as one of the bridle legs.
Sorry for the confusion. I have edited that part of the post.