MAT1375 Precalculus Spring2014 MW

Topics:

• Geometric sequences and the general formula for the nth term of a geometric sequence

• Finding the sum of the first k terms of a geometric sequence (also called the kth partial sum)

• Finding the sum of a geometric series when

Homework:

• Review the definitions and formulas, and the examples we discussed.

• Do the assigned parts of Exercises 24.1, 24.2, 24.3, 24.4

• Try doing 25.5 if you are interested (read the examples first)

• Do the WeBWorK – due by Sunday 11 PM (along with the previously assigned WeBWorK)

• Don’t forget to prepare your Final Exam review problems for Monday! You can also use the Piazza discussion board to discuss them.

See this separate post for an important announcement from the Math Department about the Final Exam.

Here is the beautiful video riffing off Fibonacci numbers, the Golden Ratio, and related things, which I mentioned in class:

https://www.youtube.com/v/kkGeOWYOFoA?fs=1&hl=en_US

(after Test 4)

Topics:

• Arithmetic sequences

• The general formula for the nth term of an arithmetic sequence:

We multiply d by (n-1) because we start adding d when we go to the second term.

• Summation notation

• Finding the sum of the first k terms of an arithmetic sequence: or

Use whichever form you find easiest to remember. To remember them more easily, recall how we derived the formula looking at Gauss’ trick for adding the first 100 natural numbers.

Homework:

• Review the definitions and notation introduced today, and the examples discussed in class. Make sure that you understand how we derived the formula for the sum of the first k terms of an arithmetic sequence given above.

• Do the assigned parts of problems 23.4 and 23.7 (first priority): 23.3 and 23.5 as time permits

• Do the WeBWorK (due next Sunday by 11 PM, but start early!)

• Look over the Final Exam Review sheet (handed out in class or available from the link in the sidebar) and choose some problems you would want to present next week on review day. You will sign up for one problem next time, but there will be the opportunity to volunteer for more, so prepare as many as you can.

Topics:

• Vectors in the plane

• Magnitude and direction angle of a vector

• Unit vectors

• Scalar multiplication

• Vector addition

• Quick introduction to sequences (Session 23, Ex. 23.2 and 23.3)

Homework:

• Review the definitions, terminology, and notation in the examples regarding vectors. Most of it should be familiar from complex numbers: we just use different names and notation.

• Do the assigned problems from Session 22

• Do the assigned parts of Exercise 23.1 [It’s a good idea to look at the terms you get and ask if they are giving an arithmetic sequence, a geometric sequence, or neither.]

• No Warm-Up because Test 4 is next time. Please see the Piazza discussion board where you can find graphs for the Test 4 review problems and also more information about which sessions the problems refer to.

• Do the WeBWorK (due Tuesday evening, the day after Test 4, by 11 PM).

Topics:

• The geometric representation of complex numbers: we represent the complex number a+bi as the point (a,b) in the coordinate plane (called “the complex plane” when we are talking about complex numbers). Better: we really think of a+bi as the vector which starts at the origin (0,0) and ends at (a,b).

• Review of operations on complex numbers.

• The absolute value (or modulus) of a complex number

Definition: |a+bi| is the distance between the point (a,b) and the origin (0,0) on the complex plane.

From the Pythagorean Theorem we find that we can compute

• The polar form of a complex number

The polar form has two coordinates:

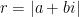
, which is the angle in standard position to the vector ending at (a,b).

We can find by using the fact that 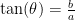, as you can see by looking at the graph.

• Changing from rectangular form (“standard form”) a+bi to polar form and vice-versa.

• Multiplying and dividing complex numbers using the polar form.

Note: I do not know of any application of complex numbers which uses the polar form with an angle in degrees. As far as I can determine, only radians are used in applications (to electrical engineering and various branches of physics). This is partly because the “angle” is usually time or some other one-dimensional quantity, not literally an angle. Also, in calculus it is much easier and more natural to work in radians. Therefore you should give all answers to the exercises in this section using radians for the angles.

For some information about the use of complex numbers in electrical engineering, and also a quick review of all of the above topics, you may want to view these documents:

Introduction to Complex Numbers in Physics/Engineering (I cannot figure out who the author of this very nice document is, but it comes from the Physics Department at College of Saint Benedict and Saint John’s University in Minnesota)

Complex Numbers and Phasors (by Professor Andrew E. Yagle, EECS 206 Instructor, Fall 2005 Dept. of EECS, The University of Michigan, Ann Arbor) [EECS = electrical engineering and computer science]

Note: The usual convention is that the angle (called the argument of the complex number) should be in the interval 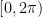. However, this is not crucial. But make sure that your angle terminates in the correct quadrant!

Homework:

• Review the definitions and examples worked in class. Take advantage of this opportunity to review finding exact values of trig functions and inverse trig functions using the basic triangles and the points on the axes from the unit circle!

• Do the assigned problems from Session 21

• Do the WeBWorK – due tomorrow by 11PM, so start early!

• No Warm-Up until next week

• There is a new review problem on WebWorK, also due tomorrow by 11 PM. Again, this is optional and will count as extra credit to your WeBWorK score if you do it.

• Don’t forget that Test 4 is scheduled for next Monday 12 May. The review problems were handed out in class and will also be available, along with the answers, on Piazza.

Topics:

• Solving the basic trig equations: , , .

The methods are developed in these examples:

Example 20.1 for 

Example 20.4 for 

Example 20.7 for 

Examples 20.3, 20.6, and 20.9 use the developed methods to solve other basic trig equations.

See the useful Summary just before Example 20.10 on p. 275

• Solving other types of trig equations by reducing them to one or more basic equations. (Examples 20.10 and 20.11)

Homework:

• Study the examples which were used to develop the methods for solving the basic trig equations. Make sure that you understand the reasoning behind them.

• Review the other examples discussed in class.

• Do the assigned problems from Session 20.

• Make sure you do the WeBWorK (assigned last time).

• No Warm-Up this time.

• Spend a few minutes every day reviewing the basics of trigonometry, and reviewing the properties of logarithms. I have posted a very short WeBWorK assignment “LogReview1”  to help in this review. It is optional and will count as extra credit in your WeBWorK score. I will post other short review assignments throughout the rest of the semester.

Topics:

• The addition, subtraction, and double angle identities for tangent

• Proving identities

• The inverse trig functions (Session 19)

• Solving the basic tangent equations

Homework:

• Review the examples discussed in class

• Review the definitions of the inverse trig functions and their properties

• Do the assigned parts of Exercises 18.1, 18.2, 18.4 (assigned previously: in 18.4 do double angle only)

• Do the assigned problems from Session 19

• Do Exercises 20.1(a), 20.2(a)

• Do the Warm-Up (due tomorrow evening by 11 PM)

• Do the WeBWorK (due next Sunday by 11 PM)

Topics:

• Finding exact values for the trig functions using knowledge of basic triangles and points on the coordinate axes

• Basic graphs of sine, cosine, and tangent and their properties

• Transformed graphs of sine and cosine functions

Here are the notes I handed out in class: MAT1375TrigGraphsFivePointMethod

• Angle addition and subtraction identities

• The double-angle identities for sine and cosine

The difference between the reference triangle and the other triangle the book uses: If you use the reference triangle, the values of the trig functions are the same for the reference angle as for the original angle, except for possible – signs (which depend on the quadrant the angle is in).

You can use either of the two triangles to find the coordinates of the point on the the terminal side, and then use the definitions of the trig functions.

Homework:

• Review the definitions of the trig functions, the unit circle picture also

• Review the examples discussed in class

• Do the assigned parts of Exercises 17.1 (exact values, not using a calculator, and practice using the basic triangles and the definition of the trig functions); 17.5, 17.6 (and as time permits, 17.3, 17.4)

• Do the assigned parts of Exercises 18.1, 18.2 (for tangent, either use that tangent = sine/cosine or look up the formula for tangent); 18.4

Topics:

• Exponential functions in applications where the rate of growth or decay (decrease) per unit time is known. (See Examples 15.6, 15.7, and 15.8)

Exponential growth and decay occur when the rate of change is a percentage of the quantity that is growing or decreasing. (Technically, we say that the rate of change is proportional to the quantity.)

If the rate of change r is known (as a percent per unit of time), then the base of the exponential function is for exponential growth, or for exponential decay. In other words,

for exponential growth

for exponential decay

• Quick review of trigonometry (to be continued): See Session 17

Note: Better names for the two basic triangles are: the isosceles right triangle, and half of an equilateral triangle. These names are better for two reasons: first, they remind you of what the triangles are, and second, they are not tying you to the degree measure of the angles. (Remember, we are trying to learn to think in radians.)

Homework:

• Reread and review the examples from Session 15 that were discussed in class.

• Learn the two basic triangles for trigonometry. I recommend that you develop them from scratch the way that I did in class. Doing this a few times over a week or so will make them stay in your memory! Also practice thinking in radians, and review the material discussed in class.

• Finish the assigned problems from Session 15

• Do the assigned parts of Exercise 17.1

• No WeBWorK or Warm-Up this time, because of the test next time. Test 3 Review answers and discussion are over on the Piazza discussion board.