Author: Sybil Shaver

See program here.

Honoring the 90th anniversary of Analog magazine.

Reminder: the Quiz tomorrow will be a one-tIme chance to raise your grade on Test 3 by solving a rational equation by clearing the denominators. (If you did the problem on Test 3 correctly, this quiz will give you a little extra credit. There are only two students this applies to!) Please read this post and also practice with the WeBWorK assignment “FractionalEquations”, problems 9, 10, and 11. (This assignment is closed, so you can read the solution and then use “show me another” for practice. Here are more video resources.

Here again is the trig identities made easier handout, with all the pretty colors. Your homework from this is to complete the problems on page 7 (not handed out in class), which are:

4) Using the method in the handout, show that:

(d) $\frac{\sin{x}\cos{x} + \sin{x}}{\cos{x} + \cos^{2}{x}} = \tan{x}$

(e) $\frac{(\sec{x} + \tan{x})(\sec{x} – \tan{x})}{\csc{x}} = \sin{x}$

(f) $\frac{\cot{x}}{\sec{x}} – \frac{\cos{x}}{\sin{x}} = \frac{\cos{x} -1}{\tan{x}}$

Also do problem 10 from the Final Exam Review sheet: MAT1275FinalReview

Possibly of interest: referring to problem 9, I looked up the ADA requirements for accessibility ramps, and this is what I found:  the maximum “tilt” of the ramp can be specified as a slope (rise to “length”, which is the same a our “run”), as a percentage (usually called the “grade”), or in degrees. The maximum slope is 1:12 which corresponds to $\frac{1}{12}$ in fraction notation. Can you figure out how this translates into $8.33\%$ ?

You may finish the WeBWorK assignment on Trig Equations: if you do this by midnight tonight, you will get full credit; anything you do after that gets 75% credit.

 

 

 

 

 

In this method, we will use the LCM of the denominators to clear (get rid of) all the the denominators in a rational equation. Make sure to use the Lowest common multiple: Your work will always be easier if you clear the denominators in the equation by multiplying by the LCM of all the denominators. So practice finding the LCM if necessary. Here is a Khan Academy video example. I did one example in class, and here is another:

Example: (this is one version of problem 9 from Test 4)

Solve $\frac{2}{x^{2} – 1} – \frac{1}{x-1} = \frac{1}{2}$

The denominators are
$x^{2} – 1 = (x+1)(x-1)$
$x-1$
$2$
The Lowest Common Multiple of the denominators is $2(x+1)(x-1)$ and remember to leave it in its factored form!

Now multiply each term on both sides of the equation by this LCM. Note: we are not changing to a common denominator. The goal is to get rid of the denominators.

$\left(\frac{2}{(x+1)(x-1)}\right) 2(x+1)(x-1) – \left(\frac{1}{x-1}\right) 2(x+1)(x-1) = \left(\frac{1}{2}\right) 2(x+1)(x-1)$

Cancel the common factors to clear the denominators:

$\left(2\right) 2 – 2(x+1) = (x+1)(x-1)$

$4 – 2x – 2 = x^{2} -1$

$0 = x^{2} + 2x  – 3$

Solve by factoring and using the zero product property:

$(x+3)(x-1) = 0$

$x+3 = 0$ or $x-1 = 0$

$x = -3$ or $x = 1$

These solve the quadratic equation, but do they solve the original rational equation? By substitution we can see that the first one works but the second one gives a zero denominator, so there is one solution to the equation: $x = -3$

—————————————-

See also: what NOT to do when solving a rational equation

Whenever you solve any type of equation, it is important NOT to divide out or “cancel” any factor which contains a variable (and so could possibly be equal to 0). If you do this you risk losing a solution to the equation!

For example, here is a thing I have witnessed: in trying to solve
$5x^{2} = 3x$
one person thought to divide both sides by $x$: (WRONG!)
$\frac{5x^{2}}{x} = \frac{3x}{x}$
$5x = 3$
$x = \frac{3}{5}$
This certainly is a solution of the original equation, as you can see by substituting it back in: the problem is that there is another solution, namely $x = 0$, which we lost when we divided out that factor. This being a quadratic equation, a safe way to solve it is to use the Zero Product Property:
$5x^{2} = 3x$
$5x^{2} – 3x = 0$
$x(5x – 3) = 0$
$

x = 0$ or $5x – 3 = 0 \implies x = \frac{

 

3}{5}$

In any case, avoid at all costs dividing both sides of any equation by an expression which might possibly be 0.

Here are notes and handouts plus a slideshow from the classes on Thursday 5 December and Monday 9 December. Please read! There is a clarification about some WeBWorK problems there. I have also updated it with two nice videos from Patrick’s Just Math Tutorials showing how to easily recall the important points in the unit circle.

Here is a reminder about your homework for tomorrow which  is not in WeBWorK.

Here is a post that links the department’s final exam review sheet.

Right about now would be a good time to review my course policies.

If you want to use Desmos as I did in class, here is the webpage. There is also an app which works very well. See the desmos.com homepage for links. Also see below!

Here is a page with some fun and informative stuff that you can enjoy reading or viewing (I hope) – including some pretty amazing graphs made using Desmos.

Here is a page with Quiz solutions (some missing)

Here is a page with Test solutions

Here is a page with links to the tutoring schedules and also other resources

Course materials including the textbook are here

 

The homework for tomorrow does not only consist of WeBWorK. We are working on an important topic for which there is no WeBWorK (yet).

Remember that you are assigned to complete parts d-f of exercises 1-3 on this handout

Proving trig identities

which were not done in class. It would be a good idea to go on and do the problems on page 7 (not handed out in class) if you can. We will return to this tomorrow BUT ONLY BRIEFLY! We have to do the “one Final Exam problem per day” schedule. So new topic tomorrow. Do your part and ASK if you get stuck.

UPDATED

First, two important notes:

* For the WeBWorK on trig equations (which has been reopened), in problems 3 and 4 there is an issue which David brought to my attention yesterday. Notice that both of these problems ask for the principal solution to a trig equation, but unlike the equations we have solved in class, they do not specify that the solution should be in $[0,2\pi)$. In that case, if the equation is of the form $\sin{x} =$ negative number or $\tan{x} =$ negative number, the principal solution is going to be the negative angle which is coterminal with the angle in our Unit Circle, which is easy to find because it’s just the negative of the reference angle!

This applies ONLY to sine and tangent (not cosine) and ONLY when we do not specify that the solutions should be in $[0,2\pi)$.

* On the matter of “Do not Google”, what to do?
First use the “Ask for help” button in WeBWorK!

Next, realize that I have already got some reliable resources linked on the resources page.

If you do go ahead and google despite all this, PLEASE send me a link to what you found so I can check it out. Remember that I am your Main Resource and I am always willing to work with you! (Plus, you might find a great resource I don’t already know about!)

—————————

These notes and handouts are (mainly) on the topics:

• Unit Circle definition of trig functions,
• Basic graphs of sine and cosine functions
• Solving trig equations using the Unit Circle
• Trig identities and proving identities: the method taught in class is specially designed to eliminate one of the big hurdles that students encounter in this topic and make it much simpler! But, you will need to practice working with rational expressions – adding (changing to a common denominator), multiplying, and reducing

Here are the handouts and other materials:

UnitCircleToFillIn

Here are two nice videos from Patrick’s Just Math Tutorials showing how to remember the important points in the Unit Circle easily: they correspond closely to what we did in class.

Unit circle first quadrant

Unit circle all quadrants

 

MAT1275-WhatsMyAngle-slideshow  (Shows how we got from the special angles in the first quadrant to each of the other quadrants by reflecting the reference triangle)

MAT1275SolvingTrigEquationsActivitiesHandout

Proving trig identities made easier (handed out in class, but this version has all the colors to help make clear what we are doing!)

——————————

Notes on the basic graphs of sine and cosine functions:

We used the unit circle to see what the graph of $y = \sin{(x)}$ looks like. Here is a Geogebra animation which shows both the sine and cosine graphs being generated by rotating around the unit circle. Remember that here x is the angle (in radians) and the coordinates of the point on the unit circle are cosine and sine.

We then looked at what happened to the graph of $y = \sin{(x)}$ when we made certain types of transformations. I suggest you graph $y = \sin{(x)}$  in Desmos and then compare to the graphs of each of the following:

$y = 2\sin{(x)}$

$y = \frac{1}{2}\sin{(x)}$

$y = -3\sin{(x)}$

$y = \sin{(2x)}$

$y = \sin{(\frac{1}{2}x)}$

$y = 3\sin{(\frac{1}{4}x)}$

We deduced from these experiments that multiplying the sine function by a number changes the amplitude of the graph, and multiplying the input angle x by a number changes the period. Specifically, $y = A\sin{(Bx)}$ has amplitude $|A|$ and period  $\frac{2\pi}{B}$ (if B is positive, which in real life applications it always is).

So considering for example $y = -5\sin{(\frac{2}{3}x)}$,

here $A = -5$ and $B = \frac{2}{3}$

so the amplitude is $|-5| = 5$ (amplitude is ALWAYS positive!)

and the period is $\frac{2\pi}{\left(\frac{2}{3}\right)} = 2\pi\left(\frac{3}{2}\right) = 3\pi$

Topics for today: (hopefully to be updated with better and more pictures)

• The two special triangles in the version where the hypotenuse is 1, and the angles are in radians. (We will try to think only in radians for the time being.) Here is a picture from another blog, but the angles are in degrees in it, alas.

 

The main thing when thinking in radians is not to keep translating into degrees (even in your head), but think about what the radian measure angles look like. One full rotation around the circle is $latex 2\pi$; half of that, a straight-line angle, is $\pi$; half of the straight-line angle is a right angle, which is $\frac{pi}{2}$.

To get the other important angles:

We can take half of a right angle, which will be $\frac{\pi}{4}$. This is the acute angle in the isosceles right triangle, because the two acute angles in a right triangle must add up to a right angle. (All 3 angles must add up to a straight line: theorem of geometry!)

We can take a third of a straight line angle, and that will be the angle of the equilateral triangle, which is $\frac{\pi}{3}$ (Again, all three angles must add up to a straight line.) When we cut the equilateral triangle in half to make a right triangle, the smallest angle must be half of $\frac{\pi}{3}$, namely it must be $\frac{\pi}{6}$.

Visualize these angles as you go through this and think about their sizes relative to each other: don’t think of degrees at all! The relative sizes are really very important also and associating them with the radian measure will help you become very fluent in radian language.

 

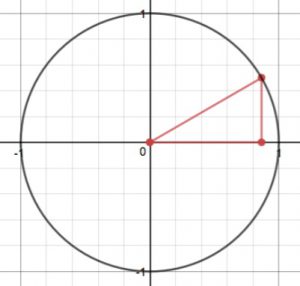
• Embedding the special triangles in the unit circle picture and reflecting them around into the four quadrants: what’s my angle?

 

In class I did this for the half-equilateral triangle and its smallest angle $\frac{\pi}{6}$. I will post the pictures I have of the process here, but they are not labeled with numbers yet.

Embedding the triangle in standard position (the vertex of the angle $\frac{\pi}{6}$ is at the origin, the adjacent side runs along the positive x-axis, and the hypotenuse extends into QI) we get this picture:

The coordinates of the vertex which lies on the unit circle were seen to be $\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$ by looking at the lengths of the sides of the triangle.

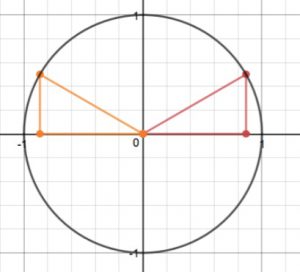
Next we reflect this across the vertical axis, and we get this picture:

In the orange triangle (which is in QII), the coordinates of the vertex which is on the unit circle are $\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$ (The first coordinate is negative because we are in QII, but otherwise these are clearly the same as they were for the first triangle.)

Now we play “what’s my angle?”. What is the standard position angle (rotation) that goes from the positive x-axis to the line segment containing this point? We can see from the picture that the angle inside the orange triangle whose vertex is at the origin is the same as it was in the first (red) triangle, namely, $\frac{\pi}{6}$. This angle is called the reference angle for the standard position angle we are looking for, and the orange triangle is its reference triangle.

The angle we are looking for forms a straight-line angle ($\pi$) when put together with that reference angle of $\frac{\pi}{6}$, so our angle must be $\frac{5\pi}{6}$. (If you take one pie and remove a sixth of the pie, how much pie is left? Same thing for $\pi$).

So the standard position angle is $\frac{5\pi}{6}$ and the coordinates of the point on the unit circle are $\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$.

 

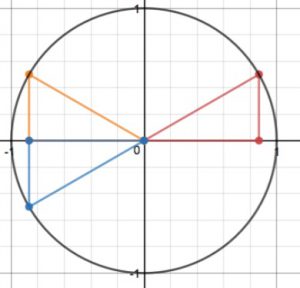
Now we reflect the orange triangle over the horizontal axis to get a triangle in QIII. The picture now looks like this:

The coordinates of the point on the unit circle for that blue triangle are $\left(-\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)$ because in QIII both coordinates are negative.

Now play “what’s my angle?”: the standard position angle here is composed of a rotation of $\pi$ plus the reference angle in the blue triangle, which is $\frac{\pi}{6}$ again of course. So our angle is $\pi + \frac{\pi}{6} = \frac{7\pi}{6}$.

 

Finally we reflect the red triangle over the horizontal axis to get a triangle in QIV. The picture now looks like this:

The coordinates of the point on the unit circle are $\left(\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)$ because in QIV the second coordinate is negative.

Now play “what’s my angle?” one more time: The angle we are looking for forms a complete rotation ($latex 2\pi$) when we put it together with the reference angle in the green triangle, so the angle we are looking for is $2\pi – \frac{\pi}{6} = \frac{11\pi}{6}$.

 

Finally we record the angles and the coordinates of those point into our big unit circle picture (which is eventually going to contain all of the important points on the unit circle).

 

Students worked with their partners on doing the same thing with the isosceles right triangles. You should finish that at home and bring it next time, and we will work on the rest of the important points then.

 

Note: There is a strong possibility of extremely sloppy weather tonight into tomorrow morning. Plan for extra travel time!

Test 4 is scheduled for tomorrow, Monday 2 December 2019, at our usual time. There will be assigned seating as there was for Test 3, but not the same seating, so try to arrive a bit early.

Some people in the class seem to think that they are only required to show up on Test days. This is false. Now would be an excellent time to review my Course Policies.

I strongly recommend that you read the post that I wrote up on the example I did in class of what NOT to do when solving a rational equation.

Something I should have mentioned there but forgot: Whenever you solve any type of equation, it is important NOT to divide out or “cancel” any factor which contains a variable (and so could possibly be equal to 0). If you do this you risk losing a solution to the equation!

For example, here is a thing I have witnessed: in trying to solve
$5x^{2} = 3x$
one person thought to divide both sides by $x$: (WRONG!)
$\frac{5x^{2}}{x} = \frac{3x}{x}$
$5x = 3$
$x = \frac{3}{5}$
This certainly is a solution of the original equation, as you can see by substituting it back in: the problem is that there is another solution, namely $x = 0$, which we lost when we divided out that factor. This being a quadratic equation, a safe way to solve it is to use the Zero Product Property:
$5x^{2} = 3x$
$5x^{2} – 3x = 0$
$x(5x – 3) = 0$
$x = 0$ or $5x – 3 = 0 \implies x = \frac{3}{5}$

In any case, avoid at all costs dividing both sides of any equation by an expression which might possibly be 0.

I also strongly recommend that you read these typed up solutions for the Quiz last Thursday, which show how to make sure you are using the relevant patterns.
MAT1275coQuiz-27Nov2019-answers

Make sure that you understand and use the important patterns: extra credit will be given to those who correctly use these patterns when they are appropriate!

• Product of conjugates (Difference of Squares)

$(A + B)(A-B) = A^{2} – B^{2}$

• Perfect square trinomial (Square of a binomial):

$(A + B)^{2} = A^{2} + 2AB + B^{2}$

$(A – B)^{2} = A^{2} – 2AB + B^{2}$

If you happen to recall that $(a + bi)(a-bi) = a^{2} + b^{2}$ you can make the solution to problem #3  on the Quiz a bit shorter, but make sure that you do it correctly in any case!

Also, the Definition of square root: $\left(\sqrt{A}\right)^{2} = A$

 

I will refer you again to the advice and resources I have posted for the previous 3 tests: remember that there are video resources available for all our topics!

By popular request, here is Jane Siberry’s song “Everything Reminds Me of My Dog”. Enjoy.