Topics for today: (hopefully to be updated with better and more pictures)
• The two special triangles in the version where the hypotenuse is 1, and the angles are in radians. (We will try to think only in radians for the time being.) Here is a picture from another blog, but the angles are in degrees in it, alas.
The main thing when thinking in radians is not to keep translating into degrees (even in your head), but think about what the radian measure angles look like. One full rotation around the circle is $latex 2\pi$; half of that, a straight-line angle, is $\pi$; half of the straight-line angle is a right angle, which is $\frac{pi}{2}$.
To get the other important angles:
We can take half of a right angle, which will be $\frac{\pi}{4}$. This is the acute angle in the isosceles right triangle, because the two acute angles in a right triangle must add up to a right angle. (All 3 angles must add up to a straight line: theorem of geometry!)
We can take a third of a straight line angle, and that will be the angle of the equilateral triangle, which is $\frac{\pi}{3}$ (Again, all three angles must add up to a straight line.) When we cut the equilateral triangle in half to make a right triangle, the smallest angle must be half of $\frac{\pi}{3}$, namely it must be $\frac{\pi}{6}$.
Visualize these angles as you go through this and think about their sizes relative to each other: don’t think of degrees at all! The relative sizes are really very important also and associating them with the radian measure will help you become very fluent in radian language.
• Embedding the special triangles in the unit circle picture and reflecting them around into the four quadrants: what’s my angle?
In class I did this for the half-equilateral triangle and its smallest angle $\frac{\pi}{6}$. I will post the pictures I have of the process here, but they are not labeled with numbers yet.
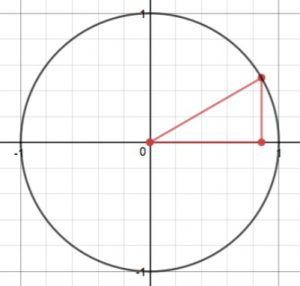
Embedding the triangle in standard position (the vertex of the angle $\frac{\pi}{6}$ is at the origin, the adjacent side runs along the positive x-axis, and the hypotenuse extends into QI) we get this picture:
The coordinates of the vertex which lies on the unit circle were seen to be $\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$ by looking at the lengths of the sides of the triangle.
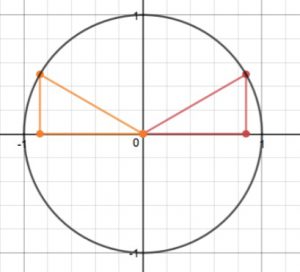
Next we reflect this across the vertical axis, and we get this picture:
In the orange triangle (which is in QII), the coordinates of the vertex which is on the unit circle are $\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$ (The first coordinate is negative because we are in QII, but otherwise these are clearly the same as they were for the first triangle.)
Now we play “what’s my angle?”. What is the standard position angle (rotation) that goes from the positive x-axis to the line segment containing this point? We can see from the picture that the angle inside the orange triangle whose vertex is at the origin is the same as it was in the first (red) triangle, namely, $\frac{\pi}{6}$. This angle is called the reference angle for the standard position angle we are looking for, and the orange triangle is its reference triangle.
The angle we are looking for forms a straight-line angle ($\pi$) when put together with that reference angle of $\frac{\pi}{6}$, so our angle must be $\frac{5\pi}{6}$. (If you take one pie and remove a sixth of the pie, how much pie is left? Same thing for $\pi$).
So the standard position angle is $\frac{5\pi}{6}$ and the coordinates of the point on the unit circle are $\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$.
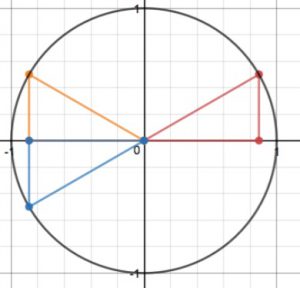
Now we reflect the orange triangle over the horizontal axis to get a triangle in QIII. The picture now looks like this:
The coordinates of the point on the unit circle for that blue triangle are $\left(-\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)$ because in QIII both coordinates are negative.
Now play “what’s my angle?”: the standard position angle here is composed of a rotation of $\pi$ plus the reference angle in the blue triangle, which is $\frac{\pi}{6}$ again of course. So our angle is $\pi + \frac{\pi}{6} = \frac{7\pi}{6}$.
Finally we reflect the red triangle over the horizontal axis to get a triangle in QIV. The picture now looks like this:
The coordinates of the point on the unit circle are $\left(\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)$ because in QIV the second coordinate is negative.
Now play “what’s my angle?” one more time: The angle we are looking for forms a complete rotation ($latex 2\pi$) when we put it together with the reference angle in the green triangle, so the angle we are looking for is $2\pi – \frac{\pi}{6} = \frac{11\pi}{6}$.
Finally we record the angles and the coordinates of those point into our big unit circle picture (which is eventually going to contain all of the important points on the unit circle).
Students worked with their partners on doing the same thing with the isosceles right triangles. You should finish that at home and bring it next time, and we will work on the rest of the important points then.