MAT2540 Discrete Structures and Algorithms II

You may work alone or in groups of at most 2. The project has 3 parts.

Part 1 (30%): Run an algorithm on an input set
You are given a fragment of pseudocode below which describes an algorithm.
(a) The pseudocode below may or may not contain an error. If there is an error, rewrite the algorithm in pseudocode with the error corrected. This may involve some judgement on your part. Highlight your change. If there is no error, skip Part 1(a).
(b) Choose an appropriate input set for the (corrected) algorithm. Show what the algorithm does with this input set. Show each step.
(c) Determine a big-O estimate for the time complexity of the (corrected) algorithm. Explain your answer.

Part 2 (50%): Translate into English
It is up to you to determine what task the (corrected) algorithm from Part 1 is performing, as well as how it accomplishes this task. Write a short essay providing a detailed description of what task the algorithm is performing, as well as a line-by-line description of how it accomplishes this task. You may quote lines directly from the pseudocode in your essay. If there was an error in the original pseudocode, include a detailed description of the error, why it causes a problem, and how your correction solves the problem. Write your essay in plain English so that it is readable by a non-expert–someone who has never taken a programming or algorithms class and who is not familiar with pseudocode.

Part 3 (20%): Translate into a programming language
Write a program that implements the (corrected) algorithm for the set of inputs you chose in Part 1 and prints the output. Include comments throughout; in particular, include a comment that shows where you have included your input set. Your program must be written in C++ or Java.

Submission instructions (note: these will be updated)
Email the following to kpoirier@citytech.cuny.edu by 11:59pm on Monday, May 16. Be sure to include your name in every file.

1. Part 1 may be completed by hand or using a computer; attach it to your email as a jpg or a pdf.
2. Part 2 must be typed using a word-processor and attached as a pdf.
3. If you are writing Part 3 in C++, save your program on cpp.sh. Create a short URL and include the link in the body of your email. If you are writing Part 3 in Java, DETAILS TBA.

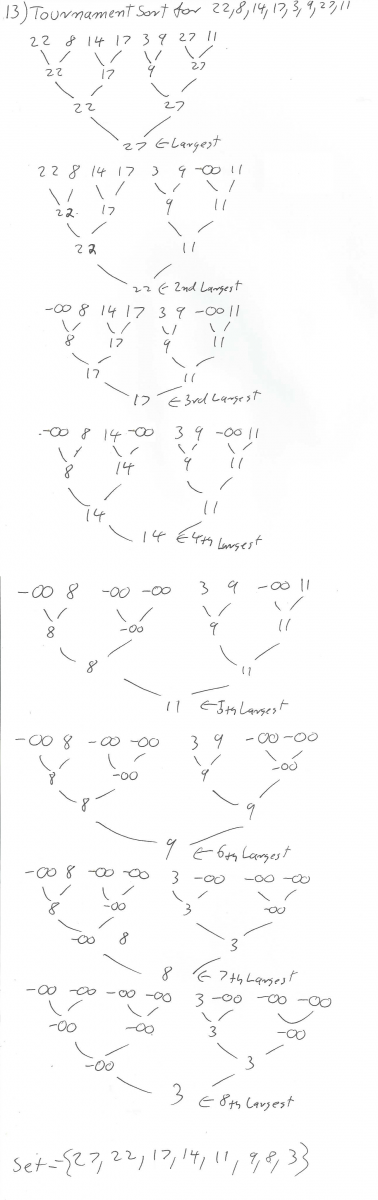
The algorithm

procedure mystery algorithm 1(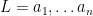: real numbers)
if 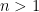then
 
 
 
 
 
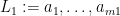
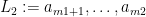
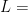  mystery algorithm 2(mystery 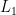algorithm 1(), mystery algorithm 1(), mystery algorithm 1()
return

procedure mystery algorithm 2(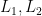 : sorted lists)
:= empty list
while 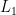and are both nonempty
  remove smaller of first elements of 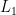and from its list; put it at the right end of
 if this removal makes one list empty then remove all elements from the other list and
 append them to
return

Edit: Mystery algorithm 1 and/or 2 may look similar to algorithms we’ve seen in class. For the project you will have to use your judgement if you are making corrections. However, if your corrected algorithm looks like one from class, then you will not receive credit for the correction. However, you may wish to use algorithms from class as a guide. Let me know if you have any questions.

Edit 2: This is not a class project. You may ask clarifying questions in the comments below, but you must work either completely independently or with your partner if you have one. (This is just a friendly reminder not to spoil it for anyone by spilling too much information about how to complete the project in the comments!)