Alright lads,
Given y=(x+sinx)^4
Find g(x) and f(x) such that f 0 g (i.e. f(g(x))) =y. Compute the derivative using chain rule.
I got the answer through observation, however I didn’t have a solid method,
We know f o g= f(g(x))=y
I have to find f(x) and g(x) such that f(g(x))=y (There are 2 ‘machines’ at work here and the order matters).
The first ‘machine/function’ is g(x)=x+sinx
Put in an ‘x’ into this ‘machine’ and out comes a ‘x+sinx’
Now for the second ‘machine’, f(x)=x4
Put in an ‘x’ into this machine and out comes a ‘x^4’
Similarly put in an ‘x+sinx’ and out comes a ‘(x+sinx)^4’
This is a how I’m thinking it in my head but I don’t know how I ‘observed’ the two functions to be f(x)=x^4 and g(x)=x+sinx. I looked at (x+sinx)^4 and ‘broke it down’ in my head. My question is, is there a routine way to calculate this for more complicated polynomials?
Finding the derivative was easy, so no worries there.




Good question, I was having the same problem figuring out, but after trying couple answers, WW finally took it.



I had:
There are of course other answers to the first question, but most of them won’t give you any help applying the chain rule. For example, if

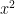

Then f(x)=
and g(x)=
fit the conditions for the first part, but they don’t let you apply the chain rule since we need to apply the chain rule to differentiate g(x). To me, that was the point of this problem. How do you break the equation into f(x) and g(x) such that you can then apply the chain rule. Observation, like you said, no special trick.