Homework #5 grades are now posted in Blackboard’s grade center. Don’t freak out that the grades are low:
- There were only three questions and I think one in particular was a little hard
- The grade you see is out of 15, not 25 as usual.
While it’s fresh in my mind, I think it’s worth commenting on your work. For the most part, the work was good, but Section 3.3 #64 was a minor disaster. (Again, don’t worry, I knew that’d be a harder one for you so I’d have been surprised if everyone got it.)
Please see my own hand-written solutions: Solutions5
I didn’t assign these questions because I care all that much about multiple roots, I just wanted you to be able to think about the kinds of arguments you can construct using derivatives and, in this case, the product rule. So you really had to think about two things while answering this question:
- Calculus
- Logic
What I mean by #2 is how to construct an argument to prove something. It’s hard to think about both things at once and I’d like to focus here on #2.
In math, when you are proving Statement A is true if and only if Statement B is true, you’re really proving two things.
- Assume Statement A is true. Use this to show that Statement B is true whenever Statement A is true. For shorthand, I’d say A implies B or if A then B. In this case, I’d say Statement A is:
has a multiple root at
and Statement B is:
has a root at
- Assume Statement B is true. Use this to show that Statement A is true whenever Statement B is true. Here, you’re showing B implies A, or if B then A.
If you haven’t worked with it before, the if and only if part of the question might throw you off. It can be particularly hard to keep track of what you’re assuming and what you’re proving. I think one reason for that is that by proving A implies B and B implies A, you’re actually saying that Statement A and Statement B are equivalent. When two things are equivalent, well, it’s hard to tell them apart! So you might accidentally assume the thing you’re trying to prove.
Compare the A if and only if B kind of result to the simpler kind A implies B. We saw an example of a result like this in class on Monday: Statement A is: 
It can also be hard to tell the difference between a proof and an assumption, or even a reason for saying something is true. I can comment more on that later, but if this kind of stuff interests you, you might like to take a class in logic.
I have question about the HW 5 solution, for the question 64 section 3.3, in the second step, where is the f(x)=(x-c)h(x) come from since the original function is f(x)=(x-c)^2(h(x)? and then the last step how do get you f(x)=(x-c)^2k(x) ? I think I probably misunderstand something.
Hi Naibing. In the second step, we’re *assuming* that c is a root of
and of 
…this means that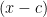 
is a factor of 
AND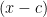 
is a factor of 
. We’re using this to *prove* that c is a multiple root of 
…this means that we want to show that 
is a factor of 
.
At the bottom of the page (the end of the proof), I could probably include some extra steps:
:
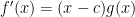(because c is a root of 
),
(because c is a root of 
).
We have two expressions for
1.
2.
Therefore,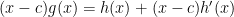
.
.
.
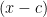is a factor of 
.
.
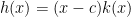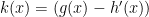, but we don’t really care what 
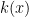is.)
Rearranging this, we have that
On the left-hand-side of this equation there are two terms, and they have a common factor:
The upshot is that
Therefore, we can write
(Here,
Since we assumed that c was a root of
, we wrote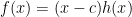 
.
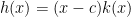, so 
and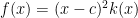 
. So we’ve *proved* that c is a multiple root of 
.
But we just showed above that
Hope that helps!