3
3a1) Neither
3a2) Odd
3a3) Neither
3a4) Even
3a5) Even
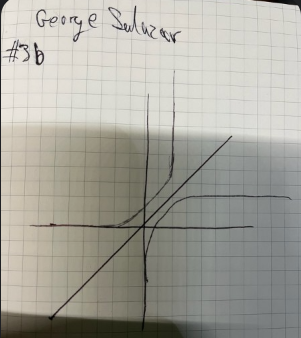
3b)
4
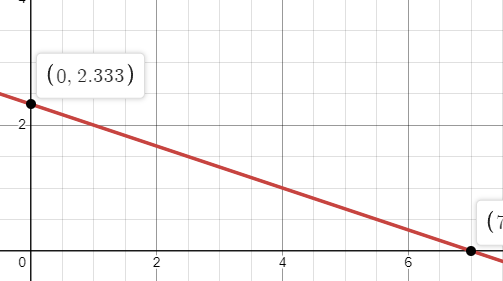
4a) y= (-1/3)x + 2(1/3)
4b) x-intercept: 7, y-intercept: 2 (1/3)
4c)
5
5a)

5b) f(x)=(x-2)^2 + 3
Professor Poirier | D366 | Spring 2024
Let f(x) and g(x) be function whose domains are real numbers. Then the domain of (f/g)x is also a real number.
False – if the denominator were to be 0, the equation will turn to be undefined.
Let g(x) be a function and assume x=2 is in the domain of g(x). Then g(2) is a real number.
True – g(2) is the output and 2 is a real number within the domain.
The inverse of a one-to-one function is always a one-to-one function
True – As it says, one-to-one is the same
Let f(x) and g(x) be polynomial functions. Then (f∘g)(x) must also be a polynomial function
True – Polynomials multiplied by polynomials will make a more complex polynomial, (x^{2}-6)(x^{2}+2x) = x^{4}+2x^{3}-6x{2}-12x
A vertical line cannot represent the graph of a function
True – It’s not a graph anymore, it’s just a vertical line at that point. x=0
10
a) f(2) = -1
b) f(1) = 2 (because of solid dot)
c) f(5) = undefined (not on graph)
d) Determine the domain of f(x). (Not fully sure how accurate this is)
(-inf,-2)U(-2,1]U(1,4]
e) Is there an x-value such that f(x) = 1? If so, find all such x-values.
x=-2 and x=1
Please let me know if you find any errors, would help me and any one else that were confused.
Coordinate with your group – post due Sunday, March 17
Congratulations on making it through Test #1!
For this week’s OpenLab assignment, you will work with your group to write up complete solutions for the test. Each member of the group is responsible for sharing solutions for two test problems so that as a group, you are sharing solutions for the whole test (if your group has 6 members, two members will post solutions for one problem each).
Group members’ contact info will be emailed to them. The group can then decide how they would like to communicate. While each individual is responsible for posting their own solutions, the group as a whole must ensure that all individual solutions are correct and complete.
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 |
| Ryan | Twaambo | Jessica | Andrew L. | Jonathan | Aaron |
| Ahmed | Mingming | Ashley | Kemanie | Melissa | Francisco |
| Andrew D. | Jordan | George | Randy | Virendra | Katherine |
| Abubakary | Yuriy | Yinson | Jahier | Matthew | Caleb |
| Ramses | Chelssie | Fiyinfoluwa | Emanuel G. | Skylar | Sara |
| Hermani |
For your individual post:
© 2025 MAT 1375 Precalculus
Theme by Anders Noren — Up ↑
Recent Comments