Class Info
- Date: Mon Dec 18
- Meeting Info: 12p-1:40p, N700
Announcements
- The final exam is in-class on Wednesday Dec 20 – see below for a list of topics/exercises to review
- I will be in my office (N724) most of the day Tuesday grading your Exam #3’s. You can drop by if you want to pick up your exam, and/or go over any topics/examples for Wednesday’s final. I plan to be there 10a-3p.
Topics
I outlined the topics/exercises from the Final Exam Review sheet you should review for the final:

Here is a text version of the list, along with with midterm and quiz exercises to review:
Skip #1
#2(a)(b): The limit definition of the derivative: Exam 3 (exercise #4)
#3(a)-(e) & #4(a)-(e): Finding derivatives using the differentiation rules: Exam 1 (#4), Exam 2 (#2), Quiz #2
Skip #5 (logarithmic differentiation)
#6(a)(b): finding the equation of a tangent line (using the derivative and the point-slope equation of the line): Exam 1 (#3), Exam 2 (#4), Quiz #2
Skip #7 (implicit differentiation)
#8(a): linear approximation: Exam 3 (#2)
#9-10 & #16-17: applied optimization: Exam #3 (#3)
#11-15: related rates: Exam 3 (#1)
#18: using the 1st and 2nd derivative for the graph: Exam 3 (#5)
Skip #19 and #20 (definite and indefinite integrals, using “antiderivatives” — the main topic of MAT1575!)




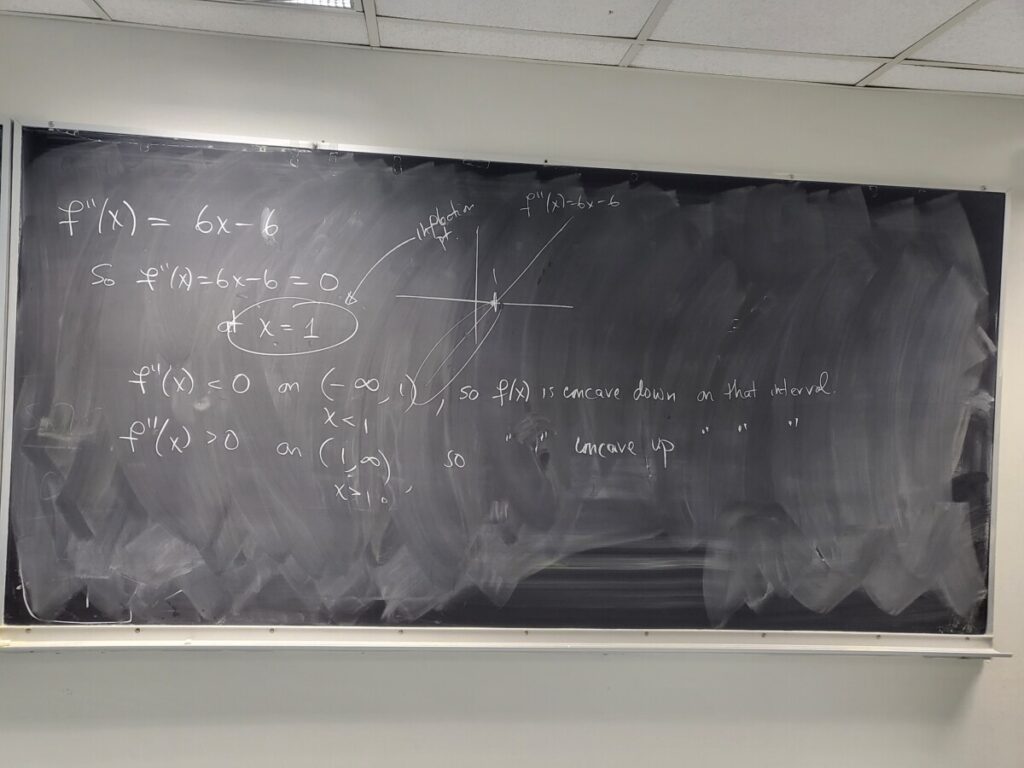



Recent Comments