Class Info
- Date: Wed Dec 6
- Meeting Info: 12p-1:40p, N700
Annoucements
WebWork:
- “Application – Monotonicity” – due Mon Dec 11
- “Application – Shapes of Polynomials” – due Mon Dec 11
Schedule for the rest of the semester:
- Exam #3 will consist of a take-home component which will be distributed in class on Monday (Dec 11) and will due the following Monday (Dec 18)
- We do not meet on Wed Dec 13 (Tues Dec 12 and Wed Dec 13 are reading days, so no classes will meet)
- There will also be an in-class exercises for Exam #3 which we will take that Monday Dec 18 (the take-home exercises will serve as preparation for the in-class exam); we will also review for the final exam that day
- The final exam is in-class on Wednesday Dec 20
- See the 1st board snapshot below for a day-by-day outline of the schedule
Topics
Here is the schedule, and also the list of topics which we have been discussing, and which will be covered on Exam #3:

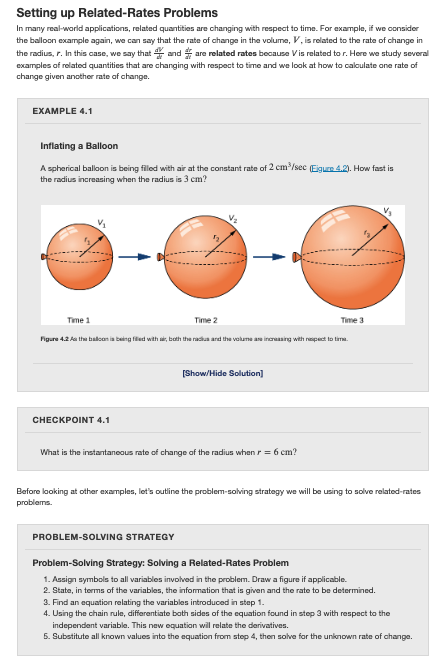
We covered “Related Rates–this is an application of the Chain Rule, for “relating” two rates of change. A typical application involves some quantity (such as the volume of same shape) which is function of some other quantity (e.g., a dimension), both of which are changing over time.
We worked through three examples from the Final Exam Review sheet:



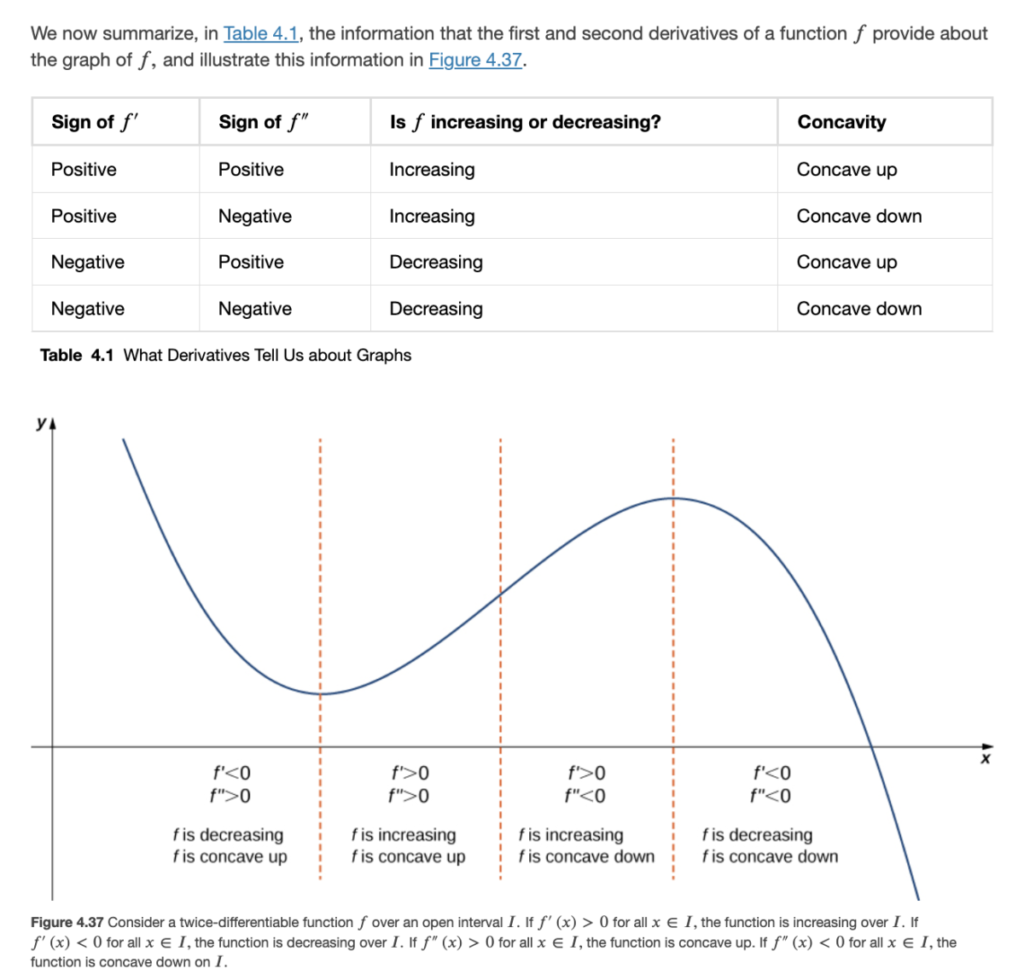
This topic is covered in Sec 4.1 of the textbook. You should read the explanation and examples there:





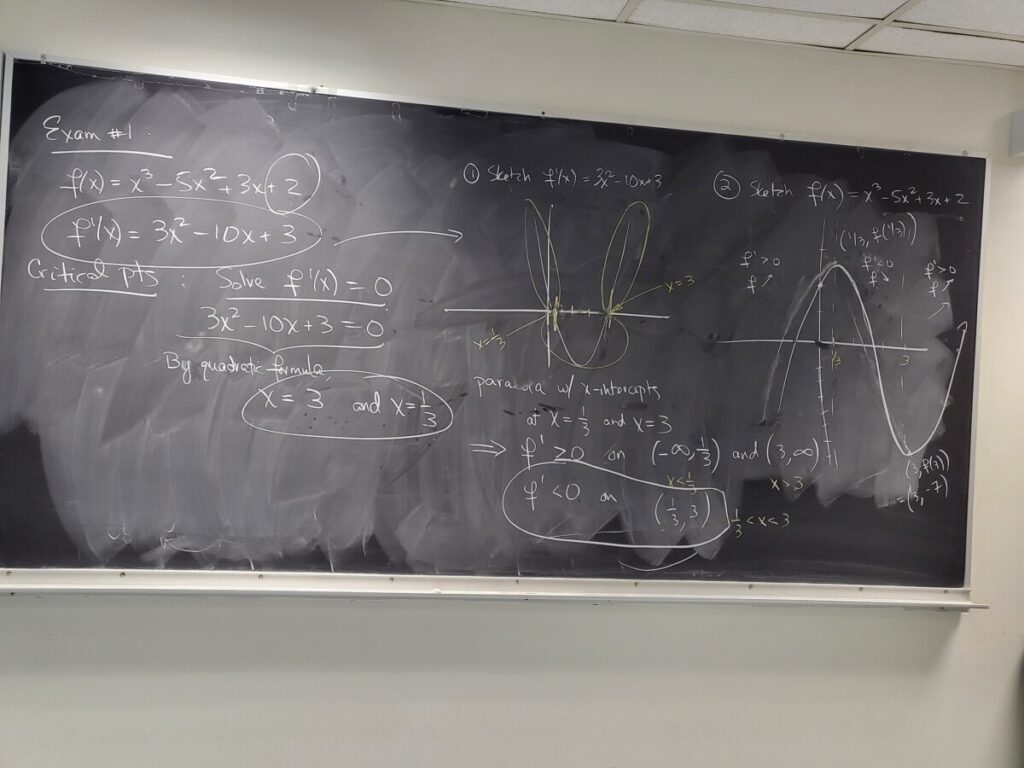






Recent Comments