We have studied how the derivative of position with respect to time gives instantaneous velocity.
To better understand this idea, I recommend reading this article by Cornell mathematician Steven Strogatz, which illustrates average and instantaneous velocities in the context of Usain Bolt’s world record setting 100-meter dash at the 2008 Olympics:
https://www.quantamagazine.org/infinite-powers-usain-bolt-and-the-art-of-calculus-20190403/
(Here is one line from the article, which should remind you of the limit definition of the derivative: “…the founders of differential calculus solved the riddle of instantaneous speed. Their intuitive solution was to define instantaneous speed as a limit — specifically, the limit of average speeds taken over shorter and shorter time intervals.”)
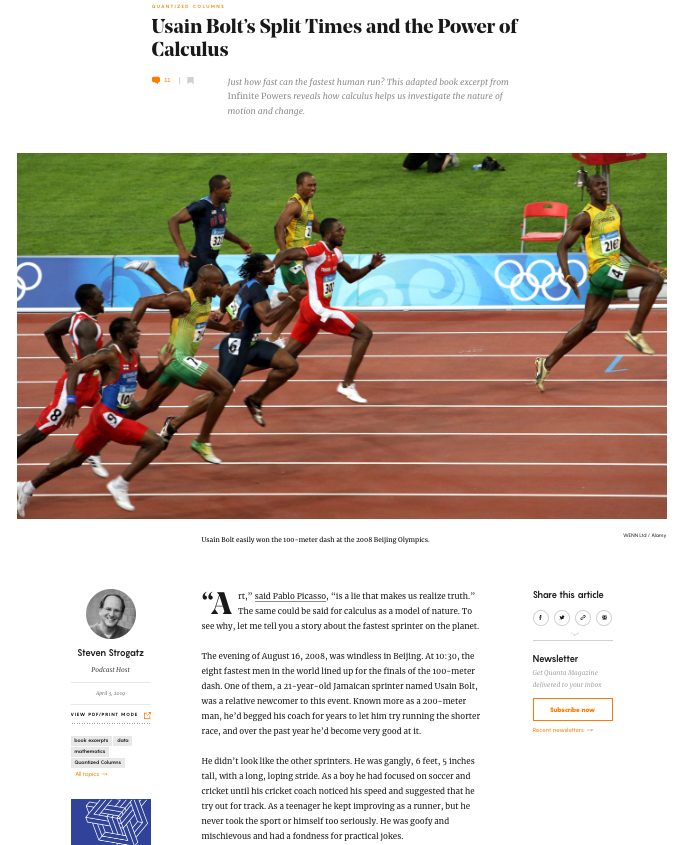
Note: this essay is actually an excerpt from Strogatz’s 2019 book Infinite Powers: How Calculus Reveals the Secrets of the Universe. I highly recommend reading this book while (or soon after) you take calculus!

Unfortunately the CityTech library doesn’t have a copy of this book, but some other CUNY libraries do:
https://cuny-ny.primo.exlibrisgroup.com/permalink/01CUNY_NY/8emd6c/alma991008499039706121



Recent Comments