The Chain Rule is the following (taken from Sec 3.6 of the textbook)–it shows how to compute the derivative of a composite function h(x) = f(g(x)):

The key to using the Chain Rule is to analyze a given composite function in terms of the “outside function” (the function f in the notation above) and the “inside function” (g above). The Chain Rule says the derivative of the composite function is “the derivative of the outside function evaluated at the inside function” (i.e., f'(g(x))) times “the derivative of the inside function” (i.e., g'(x)).
Here are a couple examples from the textbook. In Example 3.49, for h(x) = (sin x)^3, the “outside function” is the cubing function f(u) = u^3, and the “inside function” is g(x) = sin x:

What are the “outside” and “inside” functions in the following example?

Here is the Chain Rule as I presented it in class (but note that I wrote it out there applied to h(x) = g(f(x))), along with another “Checkpoint” example from the textbook:

Here are a few more Chain Rule examples we did in class:

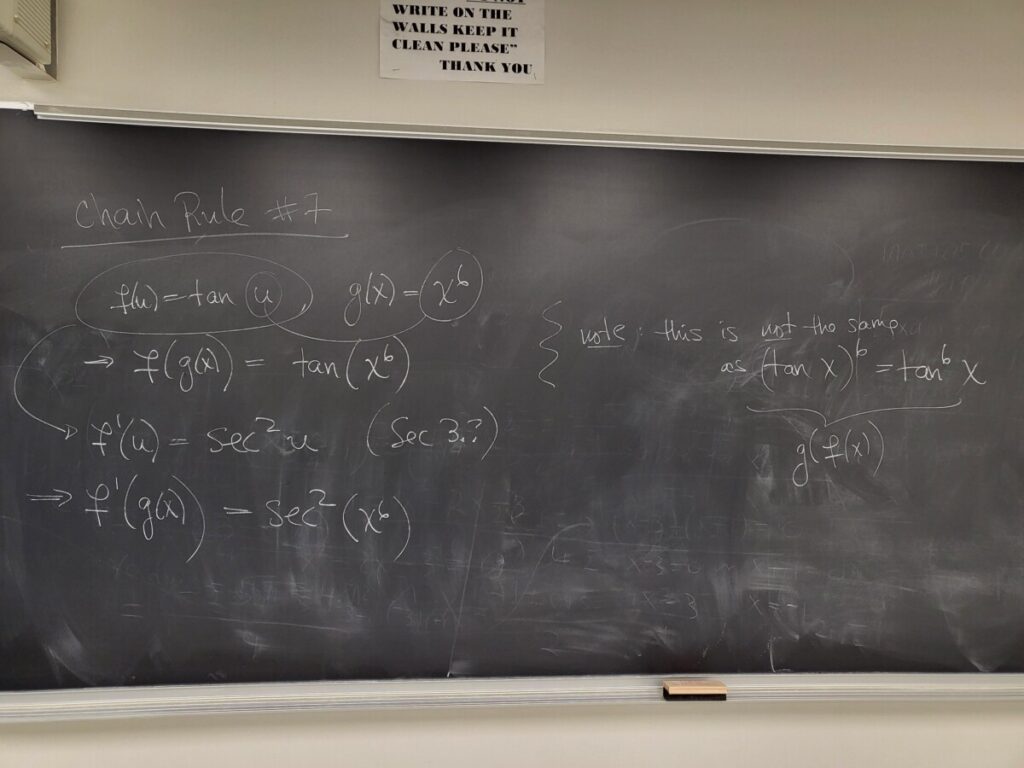




Recent Comments