Rates of Change: Average and Instantaneous

As we’ve been saying all semester, the key idea of “differential calculus” (i.e., this course) is the definition of the derivative, and how it captures “the instantaneous rate of change” (which is the same as the slope of the tangent line) as the limit of average rates of change (the limit of slopes of secant lines).

Here is the key figure again:

Note that “m_sec” is the slope of the secant line passing through the points (a, f(a)) and (x, f(x)). But this ratio (the difference quotient) is also the average rate of change of f over the x-interval (a, x)!

Here is the same figure again, as I sketched on the board last week:

Here is this concept applied to Problem 1 of “Derivatives – Rates of Change”:

Where do we get these solutions? From the following calculations:

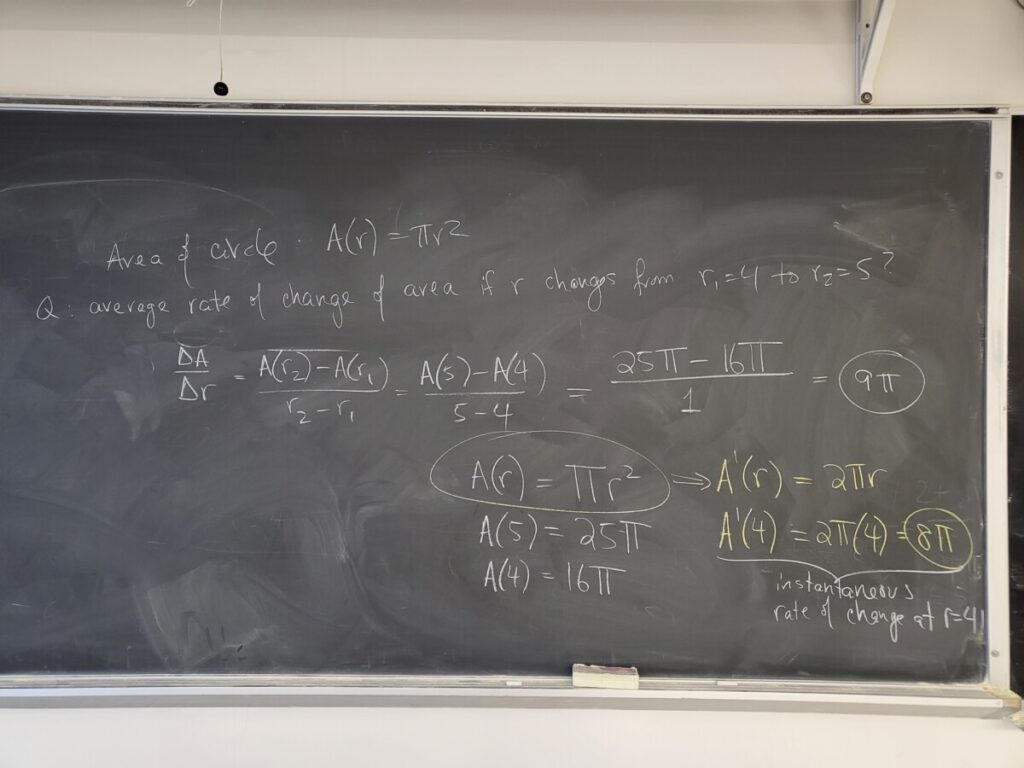
Since the derivative of a function gives us it’s instantaneous rate of change, the derivative of a “position function” s(t) gives us velocity. And the derivative of velocity, i.e., the rate of change of velocity, is gives us acceleration. Here is an excerpt from the textbook:

Here is an exercise from the WebWork set:

We get the velocity function v(t) by differentiating the given s(t), i.e., v(t) = s'(t); and we get the acceleration function a(t) by differentiating v(t), i.e., a(t) = v'(t) = s”(t).

In order to answer (b), note that the particle is “moving in the positive direction” whenever v(t) > 0. We can solve this algebraically or graphically:

Since v(t) = 3t^2 – 4t +1 = (3t – 1)(t – 1), clearly v(t) = 0 for t = 1/3 and t = 1. Since the graph of y = v(t) is a parabola opening upwards, this means v(t) > 0 for t < 1/3 and t > 1, i.e., on (-inf, 1/3) U (1, inf).

But since we are only considering t >= 0, i.e., that is the domain of s(t), as noted at the start of the exercise (t = 0 is when “time starts” for the motion of this particle), the solution is: [0, 1/3) U (1, inf).

Conversely, the solution for (c) consists of the values of t for which v(t) > 0, which is (1/3, 1).