Month: September 2022 (Page 1 of 3)

Here are some notes and hints on the “Derivatives – Limit Definition” WebWork set:

The central concept here is the definition of the derivative of a given function f(x) at a point (a, f(a)) as the limit of secant line slopes, i.e., the limit as “x approaches a” of the ratio f(x) – f(a) (the rise Δy, or sometimes called Δf) over x – a (the run Δx), i.e., Δy/Δx:

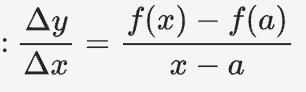
So here’s the full definition of the derivative of f at the input value a, which we call f'(a):

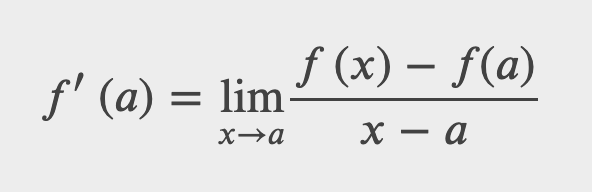
This limit of the slopes of secant lines gives us the slope of the tangent line at (a, f(a)) (in the WebWork this is called “the instantaneous slope”)

Problem 1: In this exercise, you have to numerically calculate some secant slopes Δy/Δx for the the given f(x) and the given point (a, f(a)), and then use them to

For example, in this version of the exercise, the given function is f(x) = sqrt(16-x^2) and the given point is (a, f(a)) = (2, sqrt(12)), as shown on the graph:

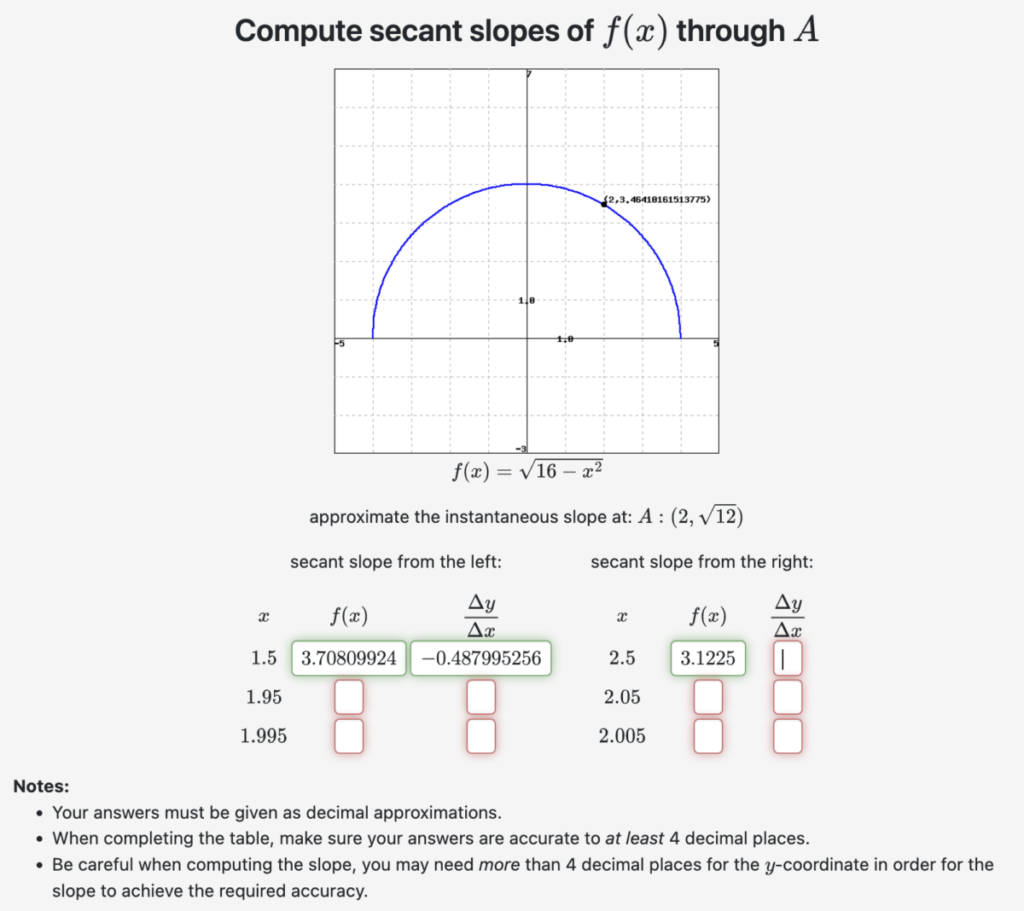
I obtained the decimal approximations shown above for x = 1.5 by using a scientific calculator (I used Desmos) to calculate f(1.5) and

Δy/Δx = [f(x) – f(a)] / [x – a] = [f(1.5) – f(2)] / [1.5 – 2]:

A good thing to do as you work through this exercise is to sketch the graph, plot each point (x, f(x)) on that graph and sketch each secant line as you compute its slope.

Problem 2: For this exercises, you have to write out Δy/Δx = [f(x) – f(a)] / [x – a] for the given function f(x) and the given point (a, f(a)).

In this case, the point is (-2, 9), and the function is the given quadratic polynomial, and I have typed in the solution for Δy/Δx:

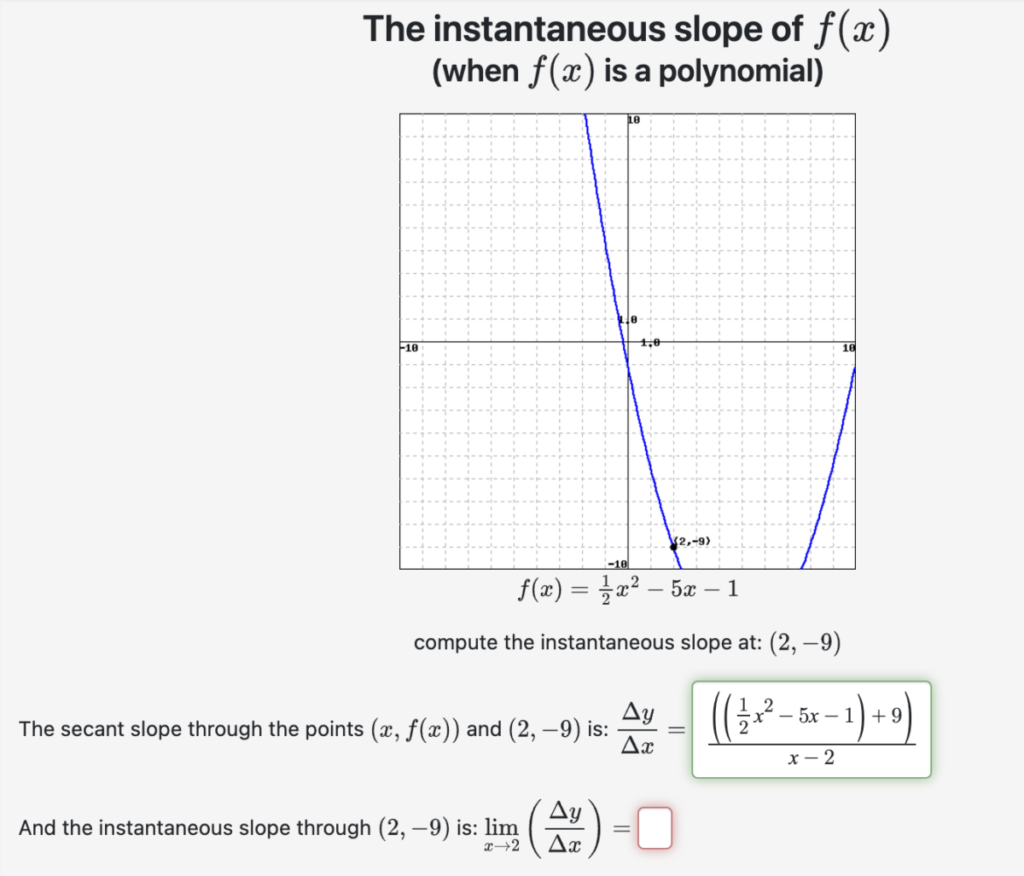
For the 2nd part, in order to find the instantaneous slope by finding the limit, recall how we found such limits by factoring the polynomial in the numerator.

In a case like this, where the leading coefficient is a fraction, I would recommend multiplying the numerator and denominator by 2 in order to make all coefficient integers, i.e., work with:

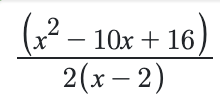
You should see that you can factor the numerator, yielding a common factor of (x-2) which you can then cancel, which allows you to evaluate the limit as x goes to 2 (i.e., just plug in x =2!).