We will have our second midterm exam on Thursday (Nov 10). To prepare for the exam:
- review the following WebWork exercises
- Derivatives – Product Rule: TBA
- Derivatives – Quotient Rule: TBA
- Derivatives – Rates of Change: #1, 3-5, 6(a)-(e), 7-9
- Derivatives – Trigonometric: 1-7
- review Quiz #2 (solutions have been uploaded to Files)
- review the following concepts:
- average rate of change/average velocity, as computed using the difference quotient (which also gives the slope of a secant line)
- instantaneous rate of change, computed using the derivative
- velocity and acceleration as first and second derivatives of position
- derivatives of sin and cos (and how to find derivatives of the other trig functions using the quotient rule)
- applying product and quotient rule, including to products and quotients involving trig functions
- finding the equation of the tangent line to y = f(x) at a point (x_1, f(x_1)) by using the point-slope equation of the line, with y_1 = f(x_1):
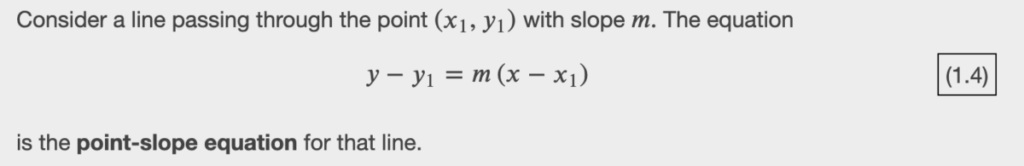
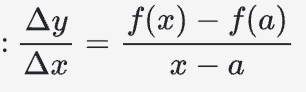


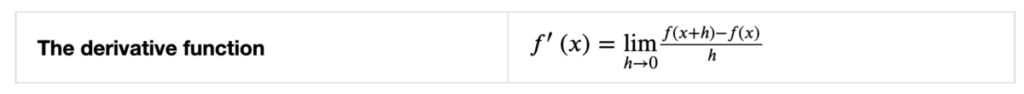




Recent Comments