Announcements
Exam #3 consists of (a) a set of take-home exercises that were handed out Wed May 15, and (b) a set of in-class exercises on Mon May 20, when the take-home exercises will also be collected. The final exam is on Wed May 22.
If you weren’t in class on Wednesday (or if you need another copy of the take-home exercises), I have uploaded a pdf to OpenLab Files.
Here is an outline of the exercises on the take-home exam:

For the take-home exercises, please study the examples we have done in class over the past few weeks–we did most of the relevant WebWork and Final Exam Review exercises in class.
The following WebWork sets will be open until Wed May 22, which contain exercises relevant for Exam #3 and for the Final Exam:
- Quadratic Equations-Quadratic Formula
- ComplexNumbers
- Rational Expressions-Complex Fractions 1
- Rational Expressions-Complex Fractions 2
- Graphs-Graphs of Quadratic Equations
- Trigonometry-Right Triangles Trigonometric Ratios
- Trigonometry-Coordinate Plane Unit Circle
Topics
We reviewed the chart of which trig ratios are positive vs negative in each quadrant:

We did another example from the Final Exam Review that uses this chart (and the definitions of the trig ratios in the coordinate plane):

We then reviewed the unit circle–the key idea being that for any angle, the x-coordinate on the unit circle is the cosine of that angle, and the y-coordinate is the sine of that angle:
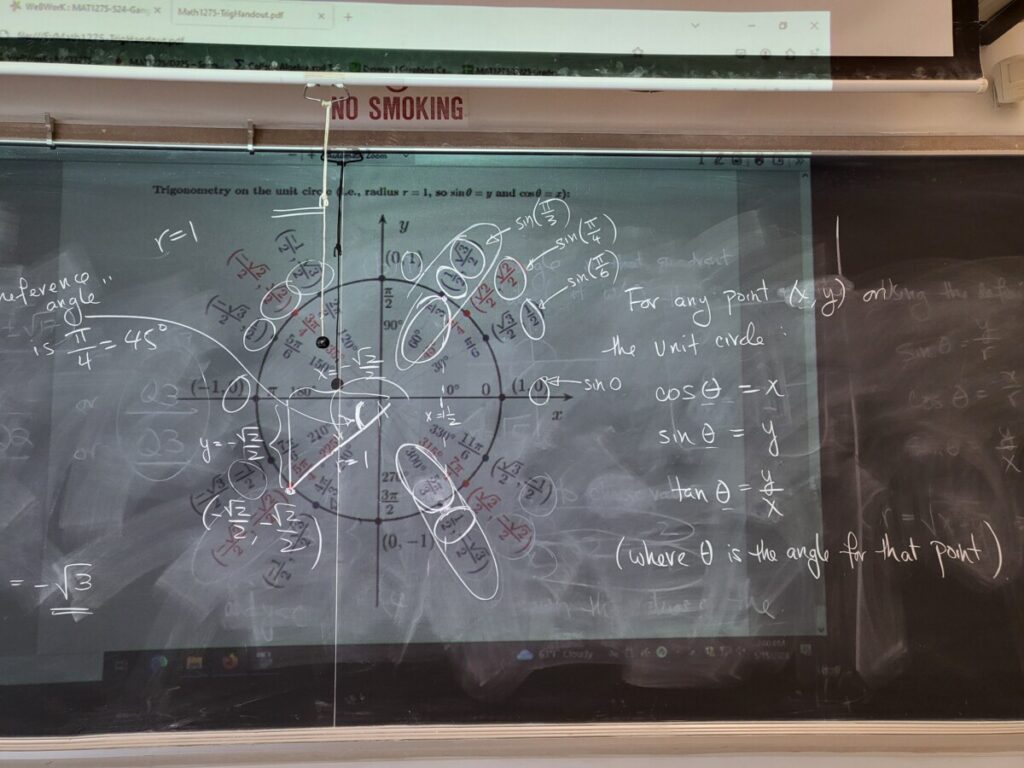
We can thus use the unit circle to find the values of the trig functions for any angle listed on the unit circle:

We can also use the unit circle “in the other direction” to solve trig equations, to solve for the angles theta which satisfy a given equation. Here is an example from the Final Exam Review:

In this example, we first did some basic algebra to isolate the trig function (cos theta) on the LHS. Then we used the unit circle to find the points at which the x-coordinate is 1/2 (pi/3 = 60 degrees and 5*pi/3 = 300 degrees). These are the angles at which cosine equals 1/2, and thus are the solutions to the given trig equation.



Recent Comments