Announcements
In order to review the topics that were on Exam #2, and to give you a chance to improve your exam score, I am giving a series of make-up exam exercises that you can use to replace some of your Exam #2 scores. The first one was at the end of this class on Monday, on the quadratic formula. The exercises on Wed May 4 will cover multiplication and division of complex numbers (similar to #5 on Exam #2); next Monday (May 8) will be complex fractions (#4 on Exam #2).
I have reopened the relevant WebWork sets so that you can complete those exercises if you didn’t previously. I have also extended some other open sets until Wed May 15:
WebWork:
- Quadratic Equations-Quadratic Formula – due Wed May 15
- ComplexNumbers – due Wed May 15
- Rational Expressions-Complex Fractions 1 – due Wed May 15
- Rational Expressions-Complex Fractions 2 – due Wed May 15
- Graphs-Graphs of Quadratic Equations – due Wed May 15
- Trigonometry-Right Triangles Trigonometric Ratios – due Mon May 13
Also, Exam #3 will be consists of (a) a set of take-home exercises, to be handed out Wed May 15, and (b) a set of in-class exercises on Mon May 20, when the take-home exercises will also be collected.
The final exam is on Wed May 22.

Topics
We first covered a remaining topic from algebra: systems of equations. First we started with a system of 2 linear equations, which we solved by the substitution method:

Then we looked at a system of equations where at least one equation is “nonlinear” (in the examples we look at, quadratic), taken from the Final Exam Review exercises:

We again used the substitution method–in this case that resulted in a single quadratic equation, which we solved by factoring. That gave the 2 x-values; we also needed to find the corresponding y-values:

We then reviewed the trig ratios, and did some additional exercises from the WebWork:
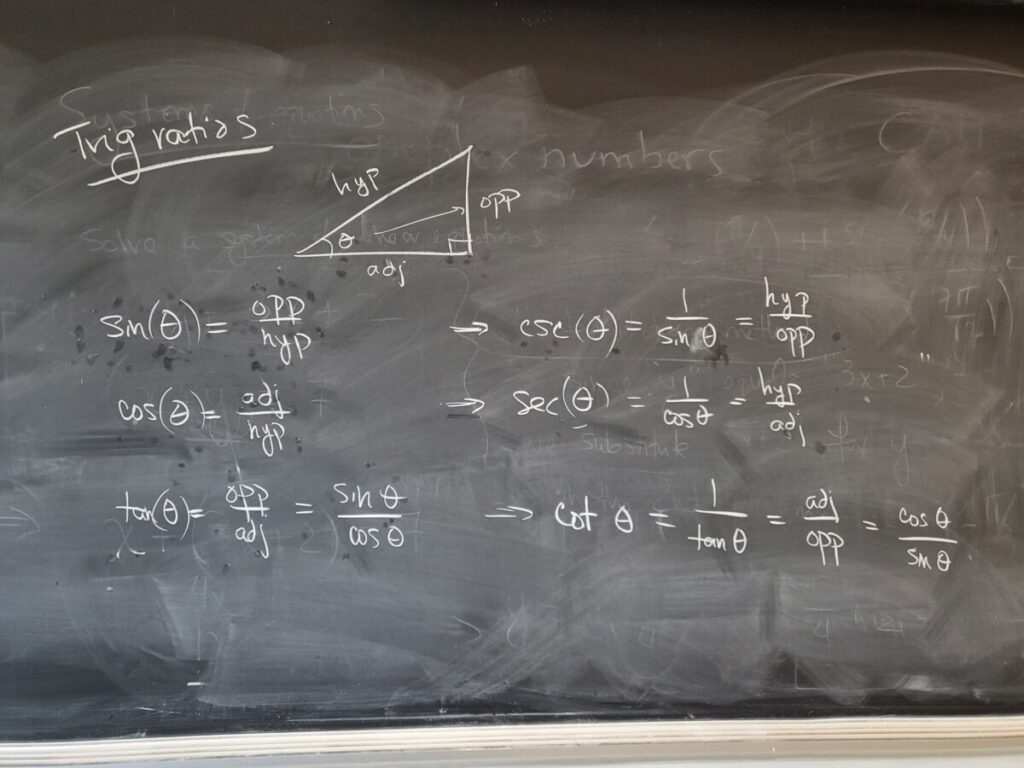
In this exercise, we needed to use the Pythagorean Theorem:

In this exercise we used the fact that the sum of all angles in any triangle is 180 degrees. We then used the trig ratios to solve for the lengths of the unknown sides:




Recent Comments