Hi everyone! Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Lesson 2: Cartesian Products and Subsets
Topic. This lesson covers:
- Sec 1.2: Cartesian Products
- Sec 1.3: Subsets
Learning Outcomes.
- Identify and manipulate ordered pairs and Cartesian products of sets.
- Identify and manipulate subsets of sets.
WeBWorK. There is 1 WeBWorK assignment on today’s material:
- Assignment1-Sec1.2-1.3
Lecture Notes:
Contents
Vocabulary
- ordered pair
- Cartesian product
- ordered triple
- Cartesian power
- subset
Cartesian Products
Definitions and Theorems
- An ordered pair is a list $(x,y)$ of two things, $x$ and $y$, enclosed in parentheses and separated by a comma.
- NOTE: unlike a set, the order of the elements is important: $(2,4)$ is NOT the same as $(4,2)$
- The Cartesian product of two sets $A$ and $B$ is another set, written $A \times B,$ and defined as $A \times B=\{(a, b): a \in A, b \in B\}$
- Theorem. If $A$ and $B$ are finite sets, $|A \times B|=|A| \times|B|$.
- An ordered triple is a list $(x,y,z)$.
- A Cartesian power, like $\mathbb{R}^{2},$ is simply shorthand for the product of a set with itself $\mathbb{R}^{2}=\mathbb{R} \times \mathbb{R}$ (similar for higher powers: $N^{3}=N \times N \times N$).
Examples: Cartesian Products
Example 1: If $A=\{p, q, r\}$ and $B=\{w, x\},$ find $A \times B$
Example 2: i) Describe the Cartesian product $\mathbb{R} \times \mathbb{R}$.
ii) If $A$ is the closed interval $[0,1]$ and $B$ is the half-open interval $[2,3),$ draw a sketch of $A \times B$
Example 3: If $A=\{3,7\}, B=\{2,4\},$ and $C=\{5,9\},$ then:
i) is $(3,2,9) \in A \times B \times C$ ?
ii) is $(3,5,2) \in A \times B \times C$ ?
VIDEO: Examples – Cartesian Products
Subsets
Definition. If $A$ and $B$ are sets and every element of $A$ is also an element of $B$, then we say $A$ is a subset of $B$ and we write $A \subseteq B$.
If this is NOT the case then we say $A$ is not a subset of $B,$ and we write $A \nsubseteq B$.
NOTE: $A \subseteq B$ means there is at least one element of A that is not an element of B.
Example 4. If $A=\{2,3,5\}, B=\{2,3,4,5,6,7,8\}$ and $C=\{1,2,3\}$
i) is $A \subseteq B$ ? Why?
ii) is $A \subseteq C$ ? Why?
iii) is $C \subseteq A ?$ Why?
iv) is $A \subseteq A$ ? Why?
v) is $\varnothing \subseteq A$ ? Why?
VIDEO: Example – Subsets
Take a moment to absorb the following two theorems. Do you believe them? Why or why not?
Theorem: Every set is a subset of itself, $A \subseteq A$
Theorem: The empty set is a subset of every set: for any set $A, \varnothing \subseteq A$
Exit Questions
Test your understanding of products and subsets by working through the following examples (selected answers are provided).
- a) If $A=\{\pi, 5\}$ and $B=\{4,7\},$ then
- i) Find $A \times B$ and $B^{2}$
- ii) is $(\pi, 7) \in A \times B ?$
- iii) is $(4,5) \in B \times A ?$ iv) is $(\pi, \pi) \in A^{2} ?$
- b) If $A=\{\{4,5,6\}, \varnothing\}$ and $B=\{N, Z,(\varnothing,\{2,7\})\},$ then
- i) is $(\{4,5,6\}, Z) \in A \times B ?$
- ii) is $(\varnothing, \varnothing) \in A \times B ?$
- iii) Find $A \times B .$ What is $|A \times B| ?$ iv) is $((\varnothing,\{2,7\}), \mathrm{N},\{4,5,6\}) \in B^{3} ?$ What product of $\mathrm{A}$ ‘s and $\mathrm{B}$’s is it an element of?
- c) Sketch each set in the plane.
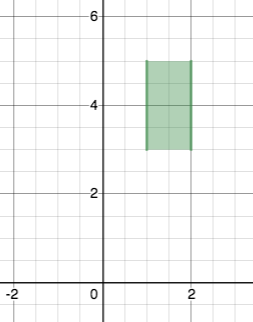
- i) $[1,2] \times(3,5)$
- ii) $\left(-1,-\frac{1}{2}\right] \times[2,3)$
- ii) $[0,1] \times{1,3,5}$
- d) Consider the set with two elements $\{5,\{5\}\} .$ True or False:
- i) $5 \in\{5,\{5\}\}$
- ii) $5 \subseteq\{5,\{5\}\}$
- iii) $\{5\}\in\{5,\{5\}\}$
- iv) $\{5\}\subseteq\{5,\{5\}\}$
- v) $\{\{5\}\}\in\{5,\{5\}\}$
- vi) {{5}}$\subseteq{5,{5}}$
- e) True or False:
- i) $\{(1,1),(2,6),(5,-1),(3,2)\} \subseteq Z \times Z$
- ii) $\mathrm{N} \times \mathrm{N} \subseteq \mathrm{R} \times \mathrm{R}$
Selected Answers
a.ii) Yes
a.iv) Yes
b.i) Yes
b.ii) No (Why not?)
c.i)
d.ii) False (there must be a SET on both sides of a $\subseteq$ sign, and 5 is not a set)
d.vi) False
e.i) True (why?)




Thanks for professor to introduce us to ready the past student’s advice for this course. we could learned a lot from them. There are only 3 classes passed and I feel easy at the beginning but some students said that the coming prove section will be difficult which we will use direct proof or contraposition proof or contradiction proof. that is funny and I am curious of that.
refer to the study method. I get some suggestions like: ready the text books and do more practice from the book, make a good note that will help us for the tests and exams. prepare lessons from class…… those are all helpful. but I thought everyone should find their own way to learning. I like to say ” practice thinking”, think more, think deeper. whether you are holding a book or not, whether you are walking or cooking, just thinking, use the brain anywhere when you want to, then you can save time and solve problems by accident.this is very interesting, you will feel the sense of success and pleasure unconsciously.