Professor Reitz has some great instructions for using
It can take some getting used to, your homework is to practice by submitting a comment on this post. Don’t worry about typing something that makes any mathematical sense, just try typing anything. Play around and make a giant mess in these comments. If something doesn’t work at first, don’t worry; just try again. (Note that your first OpenLab comment will have to be approved before it appears.)
You can mouse-over something to see what LaTeX code was. For example, mouse-over this: 
If you submit something that LaTeX doesn’t understand, it will display “formula does not parse” but you can also mouse-over that to see what was submitted.
Other resources:
- The Not So Short Introduction to
- The Comprehensive
- A shorter
- Overleaf (writing full documents and collaborating online)
- The
This is a normal comment.
OMG
$/Mu1=0=1=0=1=0=1=0=1=0=1=0=1/ngtr/Nu John Cena
You mean
$latex \Mu1=0=1=0=1=0=1=0=1=0=1=0=1/ngtr/Nu John Cena
Oh wait I mean
$latex/Mu1=0=1=0=1=0=1=0=1=0=1=0=1/ngtr/Nu John Cena
$latex/Mu1=0=1=0=1=0=1=0=1=0=1=0=1/ngtr/Nu John Cena$
Nice! If I were giving this question on a test, I’d probably put parentheses around the integrand to make it extra clear that the +5 is included: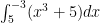
Close but it looks like your slashes are going the wrong way
I also changed your upper case Mu and Nu to lower case (the upper case ones are just M and N)
Here is a differential equation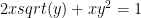
Close! To get the square root symbol, don’t forget the backslash \sqrt instead of sqrt.
(I know I said that it doesn’t matter if your math makes any sense, but I can’t stop myself from pointing out that this is not usually what we mean by “differential equation” because no derivatives appear in it. If
is a function of 
, then you could argue that 
is the zero-th derivative of itself, which would be correct, but it might make me roll my eyes.)
Agreed, I just noticed differential equation must have derivative in it, and my equation doesn’t have it . Actually when I wrote it I was focusing on the latex command more then the formula itself.
$latex\sqrt{y}2x+xy”=1 $
$ latex\sqrt{y}2x+xy”=1 $
So close! Delete the space before “latex” and add a space after it; replace your double quotation with two single ones ‘
$ latex\sqrt{y}2x+xy”=1\$
$latex\sqrt{y}2x+xy”=1\$
$latex\sqrt{y}2x+xy”=1\ $
$latex\sqrt{y}2x+xy”=1\
what a big mess I just created
one more last time
$Latex \sqrt{y}2x+xy”=1$
Haha, now just make the L on “Latex” lower case, and you’re golden!
I bet you meant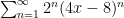
$ Latex setminus
Wow, took a lot longer than expected -.-
Looks good! Once you get the hang of typing in Latex, it becomes much easier; the first attempts always take the longest…but practicing is the point of this exercise!
Beautiful!
$latex/sqrt{x^2+1}+/sqrt[7]{x^3+5}$
Nice!
\intfrac{1}{arcsintheta}dx
$latex\intfrac{1}{arcsintheta}dx
$latex\intfrac{1}{arcsintheta}dx$
No luck for me.
$latex\int\frac{1}{arcsintheta}dx$
You got it eventually! Nice work!
It’s not important for this exercise, but I must point out that the variable in your integrand
doesn’t match your variable of integration 
, so if you were to evaluate your integral, your answer would just be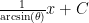 
.
Just FYI, Latex knows the trigononometric (and inverse trigonometric) functions, so there is an \arcsin macro. It might not look like a big difference, but we typically prefer the roman characters to the italic ones:
$latex\sqrt{9}$
There ya go!
$latex/sqrt{x+3}
$latex /sqrt{5}/
$latex \sqrt{15}\
$latex \sqrt{6}/
Looks good!
Lovely!
$latex \sqrt{5}
Close! Don’t forget to close up your Latex dollar signs:
$latex \sqrt{x^3 + / 1}
Nice! I’m not sure if you meant to have a fraction as a radicand. If so, you can use the Latex macro \frac:
Great!
$ Latex (n^2-3n+4)/2$
$ Latex /(n^2-3n+4)/2$
$ latex (n^2-3n+4)/2$
$ latex/(n^2-3n+4)/2
$ latex/(n^2-3n+4)/2$
So close! Move the space from before “latex” to after it.
$latex\ \If \triangle ABC \ is \ any \ triangle, \ the \ three \ bisectors \ of \ the \ interior \ angles \ of \triangleABC \ are \ concurrent. \ The \ point \ of \ concurrency \ is \ equidistant \ from \ the \ sides \ of \ the \ triangle.$
$latex\ \If \triangle ABC \ is \ any \ triangle, \ the \ three \ bisectors \ of \ the \ interior \ angles \ of \triangleABC \ are \ concurrent. \ The \ point \ of \ concurrency \ is \ equidistant \ from \ the \ sides \ of \ the \ triangle. $
$latex\ \If \triangle ABC \ is \ any \ triangle, \ the \ three \ bisectors \ of \ the \ interior \ angles \ of \triangleABC \ are \ concurrent. \ The \ point \ of \ concurrency \ is \ equidistant \ from \ the \ sides \ of \ the \ triangle. $
$latex\ If \triangle ABC \ is \ any \ triangle, \ the \ three \ bisectors \ of \ the \ interior \ angles \ of \triangleABC \ are \ concurrent. \ The \ point \ of \ concurrency \ is \ equidistant \ from \ the \ sides \ of \ the \ triangle.$
$latex\ If \triangle{ABC} \ is \ any \ triangle, \ the \ three \ bisectors \ of \ the \ interior \ angles \ of \triangle{ABC} \ are \ concurrent. \ The \ point \ of \ concurrency \ is \ equidistant \ from \ the \ sides \ of \ the \ triangle.$
$latex\ If \triangle {ABC} \ is \ any \ triangle, \ the \ three \ bisectors \ of \ the \ interior \ angles \ of \triangle {ABC} \ are \ concurrent. \ The \ point \ of \ concurrency \ is \ equidistant \ from \ the \ sides \ of \ the \ triangle.$