Test 1 #4 (Version A)

(a) Let $f(n)$ and $g(n)$ be functions from the set of positive integers to the set of real numbers. State the definition of the fact that $f(n)$ is $O(g(x))$ .

We say that $f(x)$ is $O(g(x))$ if there exists a pair of positive constants $(C,k)$ such that, for all $n>k$ , we have $|f(x)| \leq C|g(x)|$ .

(b) Use your definition from (a) to prove that $1^2+2^2+ \cdots n^2$ is $O(n^3)$ . Show all your work.

We want to find a pair of positive constants $(C,k)$ such that, for all $n>k$ , we have $|1^2+2^2+ \cdots n^2| \leq C|n^3|$ .

Assume that $n>1$ . Then we have $n$ inequalities.
$1^2 \leq n^2$ ,
$2^2 \leq n^2$ ,
…
$n^2 \leq n^2$ .

When we add up the left sides of these inequalities, we get $1^2+2^2+ \cdots n^2$ .
Adding up the right sides of these inequalities, we get $n^2+n^2+ \cdots n^2$ .
There are exactly $n$ terms in this expression, so $n^2+n^2+ \cdots n^2 = n(n^2)$ which is equal to $n^3$ .
This shows that $1^2+2^2+ \cdots n^2 \leq n^3$ whenever $n>1$ .
We also have that $1^2+2^2+ \cdots n^2 \geq 0$ , so this gives us that
$|1^2+2^2+ \cdots n^2| \leq |n^3|$ whenever $n>1$ .
In particular, we have that $|1^2+2^2+ \cdots n^2| \leq 1\cdot|n^3|$ whenever $n>1$ .
This proves that $1^2+2^2+ \cdots n^2$ is $O(n^3)$ , with witnesses $(C,k)=(1,1)$ .

This entry was posted in Test #1 Solutions. Bookmark the permalink.

The OpenLab at City Tech:A place to learn, work, and share

The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.

The OpenLab at City Tech:A place to learn, work, and share

2 Responses to Test 1 #4 (Version A)

Kate Poirier says:

March 27, 2016 at 5:06 pm

Part (a) should have been a freebie. Whether or not you’ve understood a definition from class, you should have the *precise* definition memorized. All the pieces needed to be in the right place in your answer for it to receive full credit here.

Kate Poirier says:

March 27, 2016 at 5:14 pm

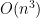Part (b) was one of the more challenging questions on the test. However, you’re given the answer here, that $1^2+ \dots n^2$ *is$ $O(n^3)$ , so that tells you exactly what you need to do: find a pair of witnesses so that your condition from (a) is satisfied.

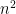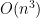One of the most wide-spread issues that I encountered while grading was that many of you appeared to be answering a completely unrelated question: that $n^2$ is $O(n^3)$ . The function 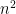$n^2$ and the function $1^2+ \dots n^2$ are completely different, so this is of no real help.

Another issue was the assumption that the function $1^2+ \dots n^2$ is a quadratic polynomial in the variable $n$ . This is not the case, even though it kind of looks like a quadratic polynomial. Compare it to $1^2+n^2$ . This *is* a quadratic polynomial. In rough terms, the difference between how it behaves and how $1^2+ \dots n^2$ behaves is that the “polynomial” $1^2+ \dots n^2$ changes when $n$ changes, while the actual polynomial $1^2+n^2$ does not.

2 Responses to Test 1 #4 (Version A)

Leave a Reply Cancel reply

Header Image

Recent Posts

Recent Comments

Archives

Categories

Meta

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons