a=superman is able to prevent evil
b= superman is impotent
c=superman is willing to prevent evil
d=superman is malevolent
e= superman exsists
f= superman prevents evil
argument form=
(a∧c)→f
¬a→b
¬c→d
¬f
e→¬b∧¬d
___________________
:.¬e
Argument =
(we have to prove ¬e)
- (a∧c)→f =”p”→f =add !f = apply modus tollens (!f∧(p→f))→!p = !p = !(a∧c)
- ¬ (a∧c) = !a V !c
¬a→b
¬c→d
e→¬(b∧d)
*i am lost after this
i know this is supposed to look like this
and pg 73 of the book has it but i dont really understand how the substituting works
this website explains more about building arguments:
http://sites.millersville.edu/bikenaga/math-proof/rules-of-inference/rules-of-inference.html

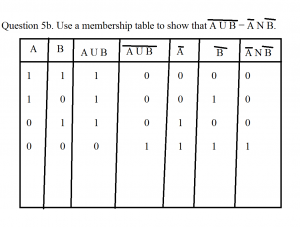
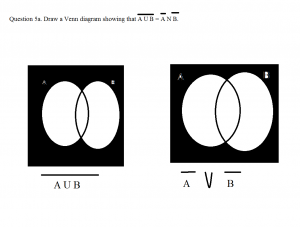



Recent Comments