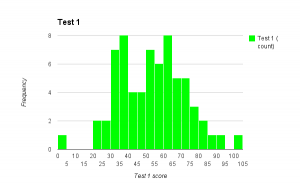
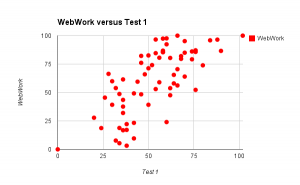
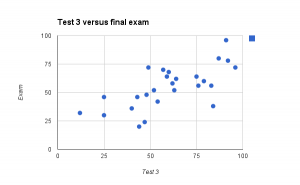
A few people have asked about the limit comparison test during office hours. It’s stated on page 564 of your text, but we can reword it in a way that might make it easier to understand.
First, imagine that instead of assuming that 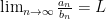 , we assumed that
, we assumed that 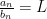 for all values of n, not just in the limit.
for all values of n, not just in the limit.
If 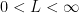 , we could write
, we could write 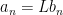 and
and  . Either way,
. Either way,  is a multiple of
is a multiple of 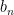 and vice versa. Multiplying a series by a constant (non-zero, non-infinite) doesn’t change whether it converges or diverges. Therefore, either both series
and vice versa. Multiplying a series by a constant (non-zero, non-infinite) doesn’t change whether it converges or diverges. Therefore, either both series 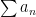 and
and 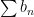 converge or they both diverge….both series have to behave the same way.
converge or they both diverge….both series have to behave the same way.
If  is very very large, then
is very very large, then 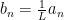 , that is,
, that is, 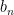 is a tiny multiple of
is a tiny multiple of  . Therefore, if you know that
. Therefore, if you know that 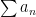 converges, then
converges, then 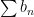 must also converge.
must also converge.
If  is very very small, then
is very very small, then 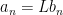 , that is,
, that is,  is a tiny multiple of
is a tiny multiple of 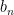 . Therefore, if you know that
. Therefore, if you know that 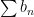 converges, then
converges, then 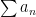 must also converge.
must also converge.
None of what I’ve said so far should sound too crazy. What’s interesting about the limit comparison test is that you don’t have to assume that 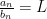 for all values of
for all values of  , you just have to assume that
, you just have to assume that 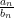 is close to
is close to  only for large values of
only for large values of  . If
. If 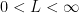 , what this says is that
, what this says is that  is eventually almost a multiple of
is eventually almost a multiple of 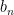 and vice versa. Therefore, either both series
and vice versa. Therefore, either both series 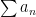 and
and 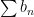 converge or they both diverge…both series have to behave the same way.
converge or they both diverge…both series have to behave the same way.
Additionally, if you let  actually approach
actually approach  , then
, then 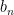 is eventually almost a tiny multiple of
is eventually almost a tiny multiple of  . Therefore, if you know that
. Therefore, if you know that 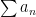 converges, then
converges, then 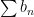 must also converge.
must also converge.
Finally, if you let  actually approach
actually approach 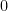 , then
, then  is eventually almost a tiny multiple of
is eventually almost a tiny multiple of 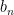 . Therefore, if you know that
. Therefore, if you know that 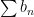 converges, then
converges, then 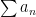 must also converge.
must also converge.
tl;dr: If the individual terms of one series are eventually almost equal to a multiple of the individual terms of another series, then both series have to behave the same way (both converge or both diverge).