Homework #5 – due March 2, 3, & 4 (Updated)

Posted on February 25, 2014 by Kate Poirier

WebWork sets Derivatives-ProductQuotient and Derivatives-Trigonometric are due Sunday night. These sets are a little long but should be straightforward after tomorrow’s class.

At the beginning of Monday’s class, please hand in the written component:
3.3 #64, 65, and 66
3.6 #49

An optional interesting problem is 3.6 #58. You might like to play around with this one, and we can talk about what you come up with, but don’t hand it in with the other exercises.

UPDATE: WebWork set Derivatives-Trigonometric is now due TUESDAY, MARCH 4 at 11:59pm. You can certainly go through most of the exercises now, but we’ll go through a bit more of the theory together on Monday in class. You can also omit 3.6 #49 from the written component. We can talk about this one in class together on Monday.

This entry was posted in Homework. Bookmark the permalink.

20 Responses to Homework #5 – due March 2, 3, & 4 (Updated)

  1. NaiBing says:
    March 1, 2014 at 12:43 pm

    For problem 9 On Web work, I got (2RV(R+V)^2-(2R+2r+2r)(V^2R))/((R+r)^4) but it is incorrect. I apply the quotient rule for this problem. I need help on this problem with strategy.

    • Kate Poirier says:
      March 2, 2014 at 11:47 am

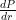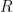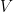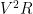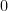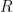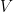      Hi NaiBing. Keep in mind that Webwork is asking for \frac{dP}{dr}. It says explicitly that R is a constant, but since you are differentiating with respect to the variable r, V is also a constant. This means that the numerator V^2R is also a constant, so its derivative is 0.. As a warm-up, try replacing the variables R and V by numbers, and the variable r by the variable x. 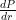Try differentiating THAT function first; you’ll be able to find your \frac{dP}{dr} using essentially the same method. Hope that helps!

  2. Nicholas Yu says:
    March 1, 2014 at 10:44 pm

    is everyone able to solve ALL of the web work? because i believe i solved the last few problems and entered them in correctly by comparing my answers to the preview and they loook 102% alike… and i did the problems multiple times and got the same answers… so i do not know is it me or WebWork is TROLLING ME! D:<

  3. Jimmy Choy says:
    March 1, 2014 at 11:00 pm

    I have issues with problem 6 – 10. I attempt multiple times to answer the questions using the rules we learned in class, but my inputs were wrong. Help me someone! 🙁

    • Kate Poirier says:
      March 2, 2014 at 12:10 pm

      Hi Jimmy. You have a few choices for how to approach problems 6 and 7. As they’re written, you’d need to use particular combinations of the product and quotient rules, since those functions are themselves particular combinations of products and quotients. (It’s important to get it all in the right order…the product of a quotient need not be the same as the quotient of a product.) You could instead simplify the function BEFORE differentiating. In these exercises, you can do a little algebra first, and then end up differentiating by a straightforward application of the quotient rule.

    • Kate Poirier says:
      March 2, 2014 at 12:18 pm

      You can ignore the hint for #8 if that helps. Find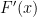 F'(x) first, and then evaluate at x=0. The point of the hint is to show you that, when you’re finding the VALUE of the derivative at a particular x-value, it can be easier to find the values of the individual pieces, and then put them together (here, using the quotient rule), than to find the derivative and then finding its value.

  5. Nicholas Yu says:
    March 2, 2014 at 4:12 pm

    is it just me? or number 7 looks funny with a separated denominator with no parenthesis and a break in the fraction line?

  6. mouhamath ciss says:
    March 2, 2014 at 5:07 pm

    its a product,,take them as f(x)*g(x)

  8. Ismail Akram says:
    March 4, 2014 at 9:13 pm

    Trig Derivatives,
    how do I express them in the form of y=mx+b and I was also given a point (x,y).
    Talking about problem 3

  9. Ismail Akram says:
    March 4, 2014 at 9:16 pm

    y=3secx-6cosx

    dy/dx= 6sinx+3tanxsecx

    given (pi/3,3)

    Then I subbed in pi/3 for x and I got m=0.21933066495 but that’s not right…

    and what’s b?

    • Ismail Akram says:
      March 4, 2014 at 9:18 pm

      it understood the answer in the form
      6sin(pi/3)+3tan(pi/3)sec(pi/3). Sooooo don’t use decimals?
      Now for b…

        • Kate Poirier says:
          March 5, 2014 at 12:59 pm

          Hey Ismail, I just saw this now. I’ll give a quick generic answer, in case anyone else is still confused.

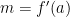          Remember that the point-slope form of the equation of a line is y-y_1 = m(x-x_1). If you’re finding the slope of a tangent line to y=f(x) at $x=a$, then x_1=a, y_1=f(a) and m=f'(a). Remember that f'(x) is a *formula* for the slope of the tangent line. If a is a *number* then f'(a) is also a number, which is the slope of the tangent.

          Usually it’s nicer to see the equation of a line in slope-y-intercept form: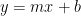 y=mx+b, so you’ll have to put a lot of your answers in this form. There are a couple of ways to find 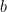b. I like to take the point-slope form from above, and solve algebraically for y. In general, rearranging the point-slope form would then look like y=f'(a)x-f'(a)a+f(a), so b=-f'(a)a + f(a).

Leave a Reply