The update to Homework #4 is that there is no update. I just checked, and given what we talked about today, you should be able to complete all the Webwork for Sunday night, and all the written work for Monday morning. There’s more to talk about from Section 3.2, but you won’t need it for the homework exercises.
Most of the questions assigned to you from 3.2 involve the relationship between the graph of a function and the graph of its derivative. This can take some getting used to at first, but once you get the hang of it, it’ll be easy. It might be helpful for you to explore the example I showed in class today more yourself. Click below.





By the way, 3.2 #98 is interesting, but it might not be completely obvious right now how it relates to limits and derivatives. We can say something more concrete later, but for now, you might like to play with this example: https://www.desmos.com/calculator/ewjdjzglsm. The question is asking about lines through the origin, so you can set b=0 and just play with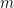 , which is really your
, which is really your 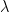 . You can add the graph
. You can add the graph 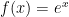 and just see how the number of intersections changes when you change the slope of your line. The person who set up this Desmos example restricted the slopes to lie between -10 and 10, but you can change these limits…just click on the numbers at the end of the slider.
and just see how the number of intersections changes when you change the slope of your line. The person who set up this Desmos example restricted the slopes to lie between -10 and 10, but you can change these limits…just click on the numbers at the end of the slider.
Use the Power Rule to compute the derivative:
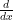
 | t=3
| t=3




=2
Use the Power Rule to compute the derivative:
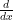
 | t=3
| t=3




=2
Use the Power Rule to compute the derivative:
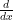
 | t=3
| t=3




=2
nothing really seems “unique” when changing c… the position just moves around in a way just so no matter what c is, when you plug in 0, you would still get the y intercept as “b”
Hi Nicholas, I’m not sure what your value of “c” is representing. Don’t forget: the question is asking about lines through the origin, with varying slopes. The y-intercept should always be 0, but you can use the online graphing tool to see what happens when you change the slope.
A solution of is unique if it’s the x-coordinate of the only point of intersection of the two graphs.
Hope that helps!
so are we comparing the f(x) and the f'(x)
AND also isn’t c any constant?
\frac{dy}{dx}
Hi NaiBing. If you’re experimenting with LaTeX, you need to add “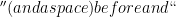 ” after what you typed in order for it to compile. If you do that,
” after what you typed in order for it to compile. If you do that, 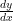 should appear!
should appear!
Oops! Let me try that comment again: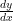 should appear!
should appear!
Hi NaiBing. If you’re experimenting with LaTeX, you need to add a-dollar-sign-and-the-word-latex (and a space) before and a dollar sign after what you typed in order for it to compile. If you do that,