This week Dr. Thiel spoke about “The Coin Change Problem”:
Title: “The Coin Change Problem”
Speaker: Johann Thiel (NYCCT)
Date/Room: Thursday Oct. 12, 2017, 12:45-2:00pm, Namm N719
Abstract:
What is the minimum number of coins needed to give someone 82 cents in change? There is a simple algorithm that solves this question for our current coin system using pennies, nickels, dimes, and quarters. (Can you figure out the algorithm?)
The more general form of this question is called the Coin Change Problem: given a list of coin denominations and a change amount, what is the minimum number of coins needed to make the change amount?
In this talk we will apply dynamic programming techniques to this problem. In particular, this talk will feature some Python programming.
Here is a
link to an introduction to dynamic programming and below you can see some of the graphs that were generated during the talk.
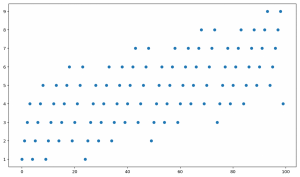
The graph below shows the minimum number of coins needed to make n cents from 1 to 100 with pennies, nickels, dimes, and quarters.
The histogram below shows the distribution of the above values.
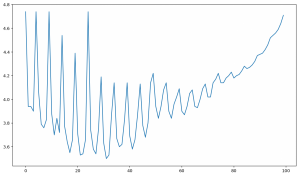
The graph below shows how the average number of coins needed to make n cents (from 1 to 100) if we add a new coin denomination to our system. The lowest average is produced by adding a 32 cent coin.
Here is a
link to a math research paper about a “better” coin system.