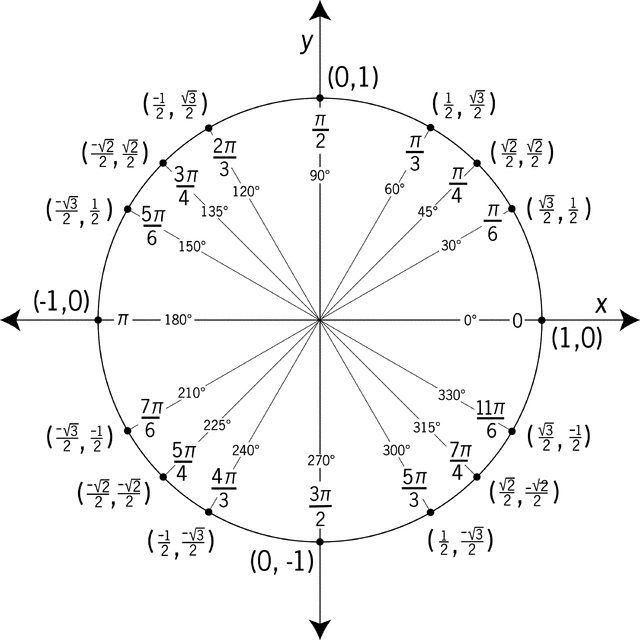
Hope you’re all having a good spring break. A reminder that we will have our third midterm exam on Tuesday, April 30 (i.e., during our first class after spring break). This exam will cover the material on exponential and logarithmic functions we have discussed over the past few weeks, but will also cover some material from earlier in the semester (in particular, there may be questions on absolute value inequalities, difference quotients, and inverse function; see below for details).
To prepare for the exam:
- review the following WebWork assignments/exercises:
- “Exponential Functions – Graphs”: #1-6
- “Logarithmic Functions – Graphs”: #1-2
- “Logarithmic Functions – Equations”: #1-4
- “Logarithmic Functions – Properties”: #1-4
- “Exponential Functions – Equations” (this set will be due Friday 5/3: even though these are due after the exam, do at least the following initial exercises before the exam): #1-3
- review solutions for Quiz #7 (solutions have been uploaded to Files)
- review Exam #1 (solutions have been uploaded to Files), specifically:
- #2 (absolute value inequalities)
- #3 (difference quotient)
- #4 (finding an inverse function)
- write out solutions for the following Final Exam Review (FER) exercises (download the FER pdf here)
- #2 (solving absolute value inequalities)
- #4 (finding the difference quotient of a given function)
- #8 (simplifying/expanding logarithmic expressions by applying the properties of logarithms)
- #9 (finding the domain, asymptote(s), and x-intercepts of a simple logarithmic function, and sketching its graph)
- #12 & #13: solving word problems involving exponential growth or decay
- #14: finding the inverse of a function
- most of the exercises on Exam #3 will be similar to the FER exercises listed above
- I will count any FER exercise solutions you hand in as extra-credit towards your homework score; you can hand these in at any time before the end of the semester