Class Info
- Date: Mon Dec 4
- Meeting Info: 12p-1:40p, N700
Topics
We reviewed how the signs of the 1st and 2nd derivatives give us information about the shape of the graph. This material is covered in Sec 4.3 and Sec 4.5. Please work on the WebWork sets “Application – Monotonicity” and “Application – Shape of Polynomials”, which cover these topics.
See also the previous Class Recap, which includes screenshots from the textbook and some videos on these topics. I also recommended working through #18 from the Final Exam Review sheet:

We outlined some of the exercises in the “Monotonicity” WebWork set, and used the last exercise to illustrate finding the critical point in order to identify the maximum of a function:

We then did two exercises from the Final Exam Review sheet on “applied optimization” (#9 and #10), which also involves finding the maximum or minimum of a given function by finding its critical point(s). The challenge in these problems is setting up the function from the given information:


You can also study the examples at the beginning of Sec 4.7: Applied Optimization.

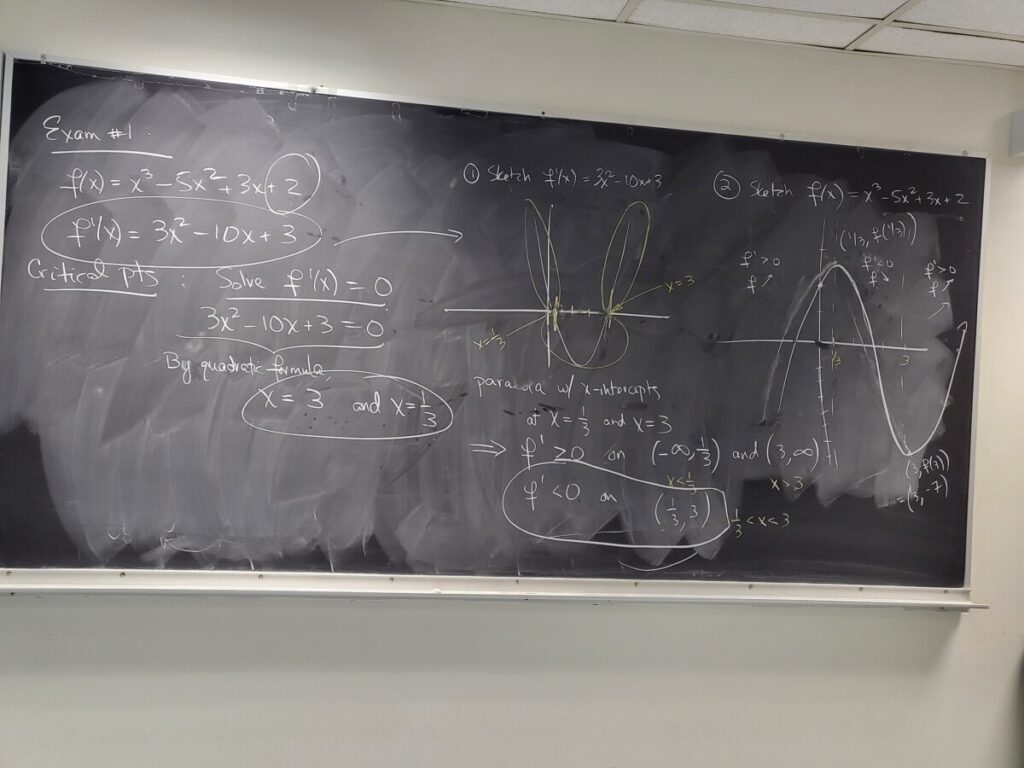




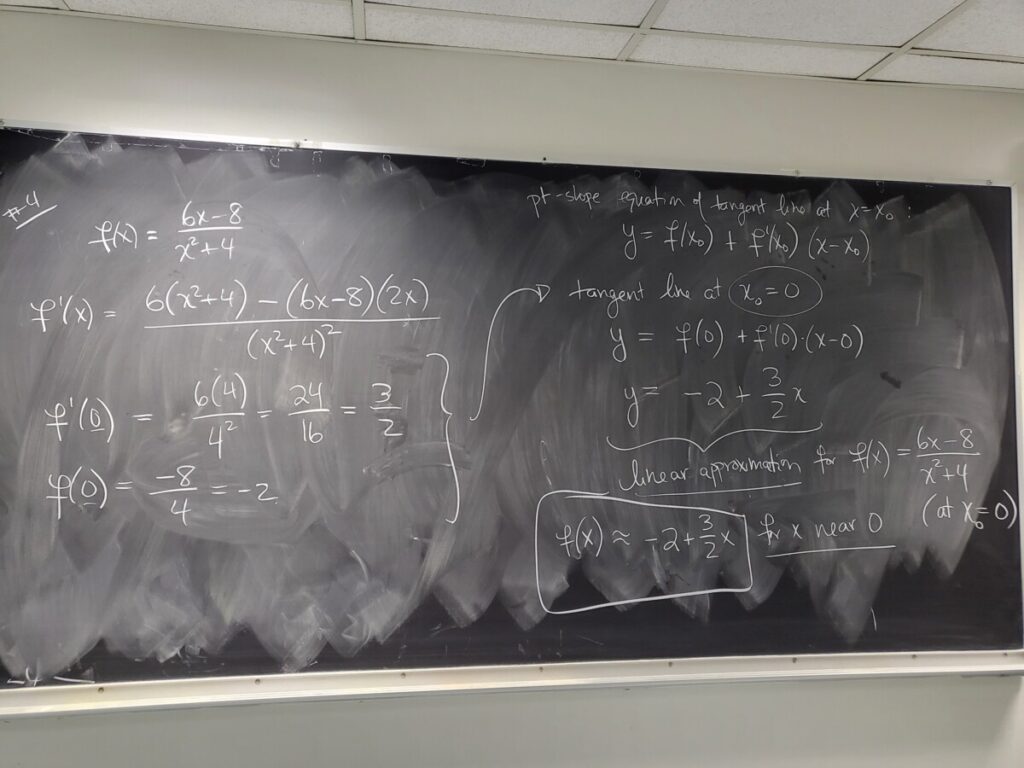
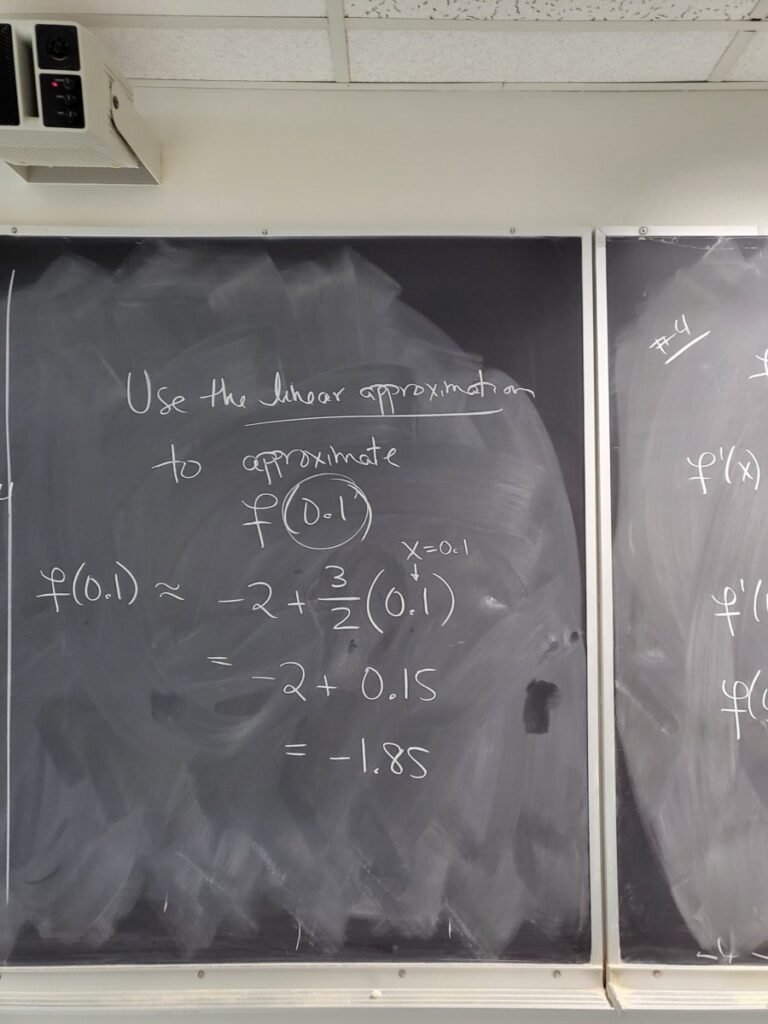




Recent Comments