Class Info
- Date: Wed Oct 25
- Meeting Info: 12p-1:40p, N700
Announcements
WebWork:
- “Derivatives – Rates of Change” — extended to Monday, Oct 30
- “Derivatives – Trigonometric” — due Friday, Nov 3
Topics
We introduced the derivatives of the trigonmetric functions (Sec 3.5).
We started by reviewing the definitions of the basic trig functions, sine and cosine, in terms of the unit circle, i.e., the circle of radius 1 centered at the origin (0,0); see Sec 1.3 for background on the trig functions. The other four trig functions–the tangent (tan), cosecant (csc), secant (sec) and cotangent (cot) are defined as ratios in terms of sin and cos:

The unit circle definition of sine and cosine leads to their graphs. Starting with the graph of y = sin x (the white curve below), we plotted the slopes of the tangent lines in yellow–we saw that it seems like the derivative sin x is cos x!

The proof that this is the case goes back to the limit definition of the derivative, applied to f(x) = sin x. We didn’t go through the details, which are presented in the textbook (which also contains a version of the graphs above):
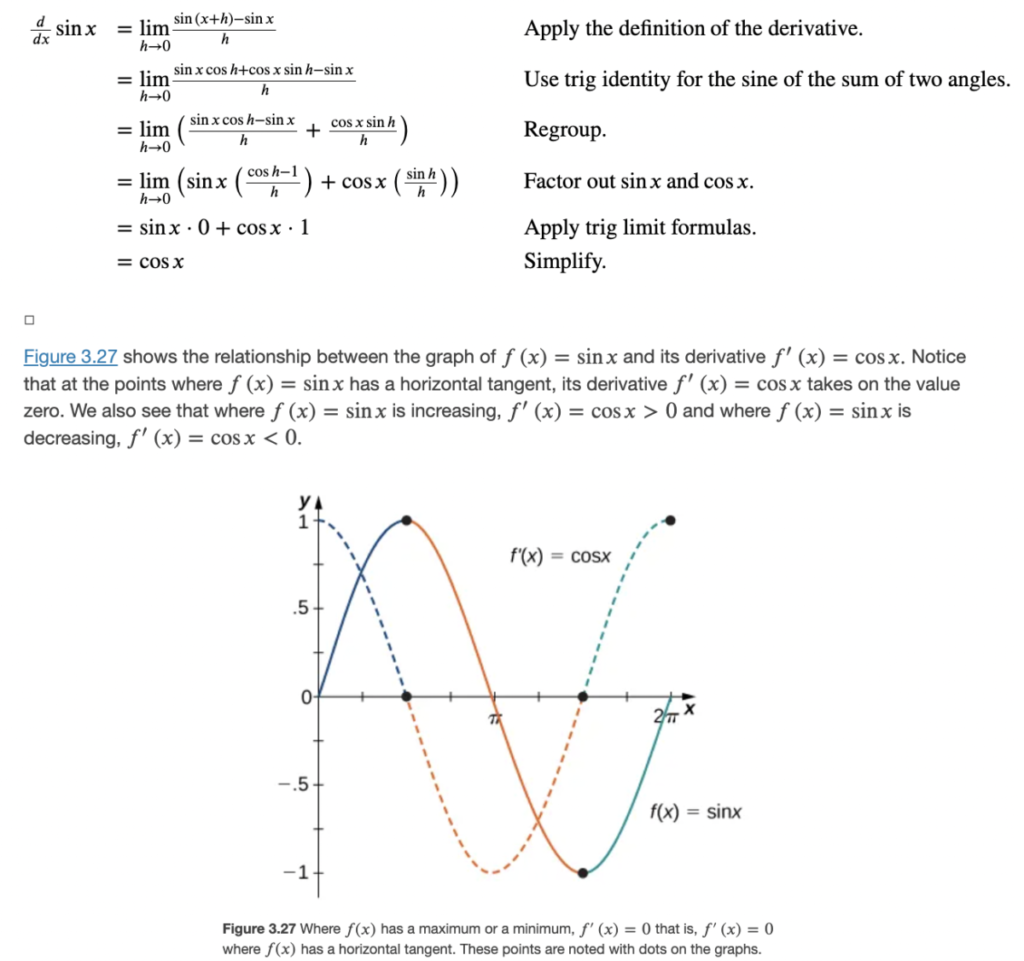
Similar reasoning leads to the derivative of cos x:

From these two derivatives, we can find the derivatives of the other trig functions using the Quotient Rule (since they are all quotients involving sin and cos!):

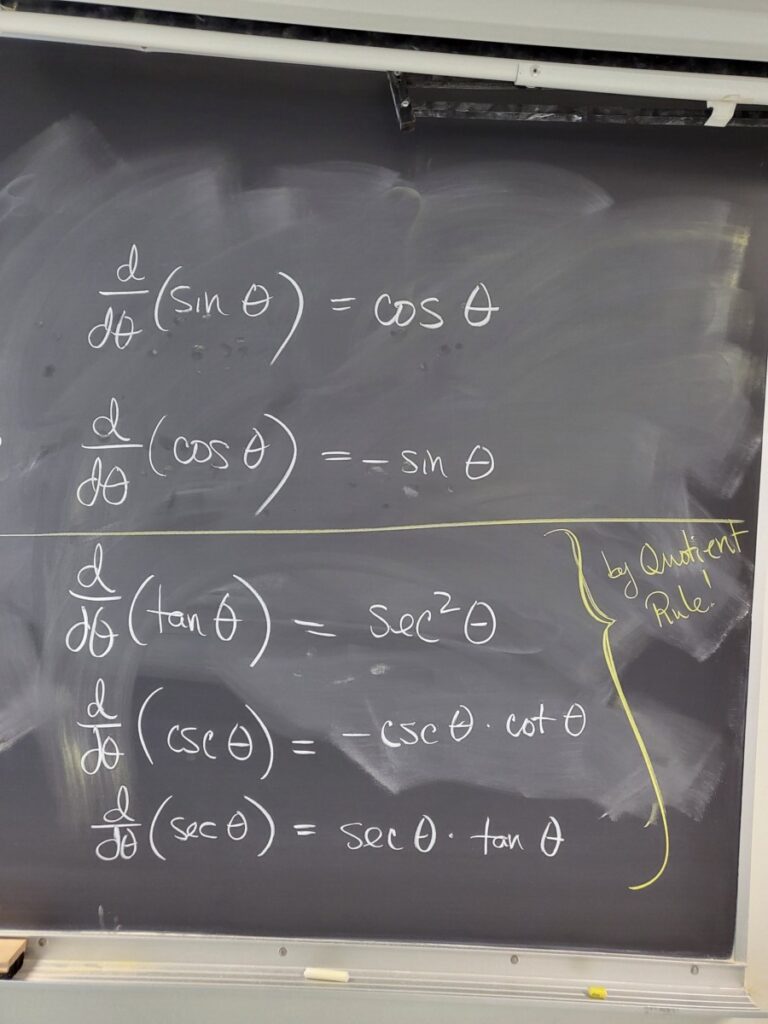
You can do the exercises in the WebWork set “Derivatives – Trigonometric” using these six derivatives, together with the differentiation rules we learned previously (Power Rule, Product Rule, Quotient Rule).
Print this page



Leave a Reply