Hi Everyone!
On this page you will find some material about Lesson 19. Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Lesson 19: Angle Measure in Radian & Trigonometry and the Coordinate Plane
Table of Contents
Resources
In this section you will find some important information about the specific resources related to this lesson:
- the learning outcomes,
- the section in the textbook,
- the WeBWorK homework sets,
- a link to the pdf of the lesson notes,
- a link to a video lesson.
Learning Outcomes. (from Coburn and Herdlick’s Trigonometry book)
- Use radians for angle measure.
- Find the radian measure of the standard angles.
- Convert between degrees and radians for nonstandard angles.
- Define the six trigonometric functions using the coordinates of a point on the terminal side of an angle.
- Analyze the signs of the trigonometric functions of an angle based on the quadrant of the terminal side.
- Evaluate the trigonometric functions of quadrantal angles.
Topic. This lesson covers
Section 3.1: Angles Measure in Radians, and
Section 1.3: Trigonometry: A View from the Coordinate Plane.
Topic. This lesson covers Section 3.1 and 1.3.
WeBWorK. There are two WeBWorK assignments on today’s material:
AngleMeasure-Radians
CoordinatePlaneTrig
Lesson Notes. (to be posted later)
Video Lesson. (to be posted later)
Warmup Questions
These are questions on fundamental concepts that you need to know before you can embark on this lesson. Don’t skip them! Take your time to do them, and check your answer by clicking on the “Show Answer” tab.
Warmup Question 1
Draw a coordinate plane. Mark Quadrant I,II,III, and IV.
Show Answer 1
Quadrant I: $x,y>0$
Quadrant II: $x<0$, $y>0$
Quadrant III: $x,y<0$
Quadrant IV: $x>0$, $y<0$
Warmup Question 2
In which quadrant is $(x,y)$, if $x<0$ and $y>0$?
Show Answer 2
Quadrant II.
Warmup Question 3
What is the hypotenuse of a right triangle whose legs measure $2$ and $4$?
Show Answer 3
By the Pythagorean Theorem, the hypotenuse is $\sqrt{2^2+4^2} = \sqrt{20} = 2\sqrt{5}$.
Review
If you are not comfortable with the Warmup Questions, don’t give up! Click on the indicated lesson for a quick catchup. A brief review will help you boost your confidence to start the new lesson, and that’s perfectly fine.
Need a review? Check Lesson ??
Quick Intro
This is like a mini-lesson with an overview of the main objects of study. It will often contain a list of key words, definitions and properties – all that is new in this lesson. We will use this opportunity to make connections with other concepts. It can be also used as a review of the lesson.
A Quick Intro to Angle Measure in Radian & Trigonometry and the Coordinate Plane
Key Words. Angle, radian, degree, terminal side, coterminal, quadrant, quadrantal angle.
$\bigstar$ In the standard position, the initial side of an angle is always on the positive $x$-axis. For positive angles, we move counter-clockwise to the terminal side of the angle.
$\bigstar$ Two angles are coterminal if they share the same initial side and terminal side.
$\bigstar$ An angle is quadrantal if when it is in standard position the terminal side is on the $x$- or $y$-axis.
$\bigstar$ An angle can be measured in degrees or radians.
$$180^\circ =\pi\rad$$

(picture taken from Precalculus’ textbook by Tradler and Carley)
(on the coordinate plane several angles are labeled indicating their measures in degrees and radians:
$$0=0^\circ, \dfrac{\pi}{6}=30^\circ, \dfrac{\pi}{4}=45^\circ, \dfrac{\pi}{3}=60^\circ,$$
$$ \dfrac{\pi}{2}=90^\circ, \dfrac{2\pi}{3}=120^\circ, \dfrac{3\pi}{4}=135^\circ, \dfrac{5\pi}{6}=150^\circ, \pi=180^\circ, $$
$$\dfrac{7\pi}{6}=210^\circ, \dfrac{5\pi}{4}=225^\circ, \dfrac{4\pi}{3}=240^\circ, $$
$$\dfrac{3\pi}{2}=270^\circ, \dfrac{5\pi}{3}=300^\circ, \dfrac{7\pi}{4}=315^\circ,\dfrac{11\pi}{6}=330^\circ .)$$
$\bigstar$ Let $P(a,b)$ be a point on the terminal side of angle $x$ with $r=\sqrt{a^2+b^2}>0$.
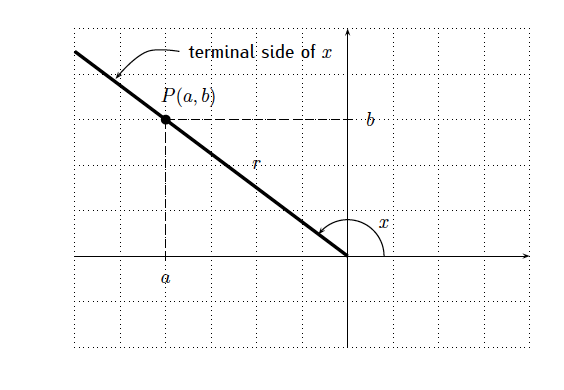
(picture taken from Precalculus’ textbook by Tradler and Carley)
(on the coordinate plane an angle $x$ in standard position has a terminal side on QII, $P(a,b)$ is a point on the terminal side, the distance between $P(a,b)$ and the origin is $r$.)
Then
$$\sin x=\dfrac{b}{r}, \quad \cos x =\dfrac{a}{r}, \quad\tan x =\dfrac{b}{a}. $$
$\bigstar$ Note that
$\sin x=\dfrac{b}{r}$ is positive when $b>0$, so QI and QII
$\cos x = \dfrac{a}{r}$ is positive when $a>0$, so QI and QIV
$\tan x = \dfrac{b}{a}$ is positive when either $a,b>0$ or $a,b<0$, so QI and QIII

(picture taken from Precalculus’ textbook by Tradler and Carley)
(on the coordinate plane an angle the four quadrants are marked, indicating which trig functions ($\sin x, \cos x, \tan x$) are positive or negative in each one of them)
Video Lesson
Many times the mini-lesson will not be enough for you to start working on the problems. You need to see someone explaining the material to you. In the video you will find a variety of examples, solved step-by-step – starting from a simple one to a more complex one. Feel free to play them as many times as you need. Pause, rewind, replay, stop… follow your pace!
Video Lesson
to be posted later
Try Questions
Now that you have read the material and watched the video, it is your turn to put in practice what you have learned. We encourage you to try the Try Questions on your own. When you are done, click on the “Show answer” tab to see if you got the correct answer.
Try Question 1
Convert $\theta = 210^{\circ}$ to radians in exact form.
Show Answer 1
$\theta = 210^{\circ}= 210\cdot\dfrac{\pi}{180} = \dfrac{210\pi}{180} = \dfrac{7\pi}{6} \text{ rad}$
Try Question 2
Find the coterminal angle with $\theta = 590^{\circ}$ whose measure is between $-180^{\circ}$ and $180^{\circ}$.
Show Answer 2
Since $-180<-130<180$, the answer is $-130^{\circ}$.
Try Question 3
Let $\theta$ be an angle in standard position with $P(x,y) = (6,-8)$ on its terminal side. Find the six trigonometric values of $\theta$.
Show Answer 3
If $P(x,y) = (6,-8)$, then $x=6$ and $y=-8$. Then
\[r=\sqrt{x^2+y^2} = \sqrt{6^2+(-8)^2} = \sqrt{36+64} = \sqrt{100} = 10.\]
Thus
$$\cos\theta = \dfrac{x}{r} = \dfrac{6}{10} =\dfrac{3}{5},$$
$$\sin\theta= \dfrac{y}{r} = \dfrac{-8}{10}=-\dfrac{4}{5}, $$
$$\tan\theta= \dfrac{y}{x} = \dfrac{-8}{6}=-\dfrac{4}{3}. $$
The quadrant is II where $x<0$ and $y>0$. We have that $y=4$, $r=5$ and
\[x = -\sqrt{r^2-y^2} = -\sqrt{25-16}=-\sqrt{9} = -3. \]
So
$$\cos \theta = \dfrac{x}{r} = -\dfrac{3}{5}, \qquad \tan\theta = \dfrac{y}{x} = -\dfrac{4}{3}, $$
$$\sec \theta = \dfrac{1}{\cos\theta} = -\dfrac{5}{3}, \qquad \csc\theta = \dfrac{1}{\sin\theta} = \dfrac{5}{4}, $$
$$\cot\theta = \dfrac{1}{\tan\theta} = -\dfrac{3}{4}.$$
WeBWorK
You should now be ready to start working on the WeBWorK problems. Doing the homework is an essential part of learning. It will help you practice the lesson and reinforce your knowledge.
WeBWork
It is time to do the homework on WeBWork:
AngleMeasure-Radians
CoordinatePlaneTrig
When you are done, come back to this page for the Exit Questions.
Exit Questions
After doing the WeBWorK problems, come back to this page. The Exit Questions include vocabulary checking and conceptual questions. Knowing the vocabulary accurately is important for us to communicate. You will also find one last problem. All these questions will give you an idea as to whether or not you have mastered the material. Remember: the “Show Answer” tab is there for you to check your work!
Exit Questions
- How can we divide up the unit circle and counting to find the location of $5\pi/3$ without converting to radians? Draw a picture.
$\bigstar$ Given $\sin\theta = \dfrac{4}{5}$ and $\cos \theta <0$, find the other five trigonometric values of $\theta$.
Show Answer
The quadrant is II where $x<0$ and $y>0$. We have that $y=4$, $r=5$ and
\[x = -\sqrt{r^2-y^2} = -\sqrt{25-16}=-\sqrt{9} = -3. \]
So
$$\cos \theta = \dfrac{x}{r} = -\dfrac{3}{5}, \qquad \tan\theta = \dfrac{y}{x} = -\dfrac{4}{3}, $$
$$\sec \theta = \dfrac{1}{\cos\theta} = -\dfrac{5}{3}, \qquad \csc\theta = \dfrac{1}{\sin\theta} = \dfrac{5}{4}, $$
$$\cot\theta = \dfrac{1}{\tan\theta} = -\dfrac{3}{4}.$$
Need more help?
Don’t wait too long to do the following.
- Watch the additional video resources.
- Talk to your instructor.
- Form a study group.
- Visit a tutor. For more information, check the tutoring page.



