Hi Everyone!
On this page you will find some material about Lesson 17. Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Lesson 17: Angle Measure and Special Triangles & The Trigonometry of Right Triangles
Table of Contents
Resources
In this section you will find some important information about the specific resources related to this lesson:
- the learning outcomes,
- the section in the textbook,
- the WeBWorK homework sets,
- a link to the pdf of the lesson notes,
- a link to a video lesson.
Learning Outcomes. (from Coburn and Herdlick’s Trigonometry book)
- Use the vocabulary associated with a study of angles and triangles.
- Find and recognize coterminal angles.
- Find fixed ratios of the sides of special triangles.
- Find values of the six trigonometric functions from their ratio definitions.
- Bridge the two definitions of the trigonometric functions by positioning a right triangle in the coordinate plane.
- Use cofunctions and complements to write equivalent expressions.
Topic. This lesson covers
Section 1.1: Angle Measure and Special Triangles, and
Section 2.1: A Right Triangle View of Trigonometry.
WeBWorK. There are two WeBWorK assignments on today’s material:
SpecialTriangles
TrigonometryRatios
Lesson Notes.
Video Lesson.
Video Lesson 17 (based on Lesson 17 Notes)
Warmup Questions
These are questions on fundamental concepts that you need to know before you can embark on this lesson. Don’t skip them! Take your time to do them, and check your answer by clicking on the “Show Answer” tab.
Warmup Question 1
In a right triangles, if one of the acute angles measures $30^\circ$, what is the measure of the other angle?
Show Answer 1
The sum of the angles in a triangle is $180^\circ$. In a right angle with an acute angle of $30^\circ$, the third angle is
$$180^\circ-90^\circ-30^\circ=60^\circ$$
Warmup Question 2
Solve for $x$
$$\dfrac{3}{x}=\dfrac{\sqrt 3}{7}.$$
Show Answer 2
$$\dfrac{3}{x}=\dfrac{\sqrt 3}{7}$$
$$\sqrt 3 x=21$$
$$x=\dfrac{21}{\sqrt 3}$$
$$x=\dfrac{21\sqrt 3}{\sqrt 3\sqrt 3}$$
$$x=\dfrac{21\sqrt 3}{3}$$
$$x=7\sqrt 3$$
Review
If you are not comfortable with the Warmup Questions, don’t give up! Click on the indicated lesson for a quick catchup. A brief review will help you boost your confidence to start the new lesson, and that’s perfectly fine.
Need a review? Check Lesson ??
Quick Intro
This is like a mini-lesson with an overview of the main objects of study. It will often contain a list of key words, definitions and properties – all that is new in this lesson. We will use this opportunity to make connections with other concepts. It can be also used as a review of the lesson.
A Quick Intro to Special Triangles
Key Words. Similar triangles, special triangles, 30-60-90, 45-45-90, leg, hypotenuse.
There are two triangles that are called special, because their sides are in a special proportion.
$\bigstar$ $30-60-90$
This is a right triangle whose acute angles are $30^\circ$ and $60^\circ$. When the hypotenuse is $2$,
$\bullet$ the side opposite to $30^\circ$ is the short leg and has length $1$
$\bullet$ the side opposite to $60^\circ$ is the long leg and has length $\sqrt 3$.
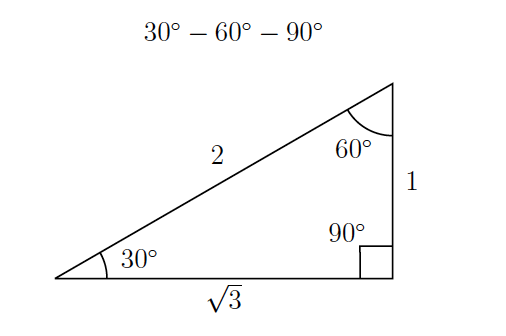
Any $30-60-90$ triangle is similar to the above triangle. If we know one of the sides of a $30-60-90$ triangle, one can use the ratios to find the two other sides.
$\bigstar$ $45-45-90$
This is a right triangle whose acute angles are both $45^\circ$, so it is isosceles. When the legs measure $1$, the hypotenuse measures $\sqrt 2$.
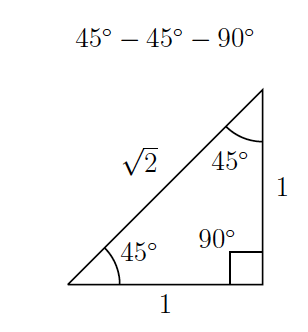
Any $45-45-90$ triangle is similar to the above triangle. If we know one of the sides of a $45-45-90$ triangle, one can use the ratios to find the two other sides.
Video Lesson
Many times the mini-lesson will not be enough for you to start working on the problems. You need to see someone explaining the material to you. In the video you will find a variety of examples, solved step-by-step – starting from a simple one to a more complex one. Feel free to play them as many times as you need. Pause, rewind, replay, stop… follow your pace!
Video Lesson
In the video you will see
- an example of a $45-45-90$ triangle with sides measuring $4$, $4$ and $4\sqrt 2$
- an example of a $30-60-90$ triangle with sides measuring $5$, $5\sqrt 3$ and $10$
- how to find the missing sides of a $30-60-90$ triangle whose long leg measures $2$
- how to find the missing sides of a $45-45-90$ triangle whose hypotenuse measures $3$
Try Questions
Now that you have read the material and watched the video, it is your turn to put in practice what you have learned. We encourage you to try the Try Questions on your own. When you are done, click on the “Show answer” tab to see if you got the correct answer.
Try Question 1
Find $x$ and $y$. Leave the answer in simplest radical form.
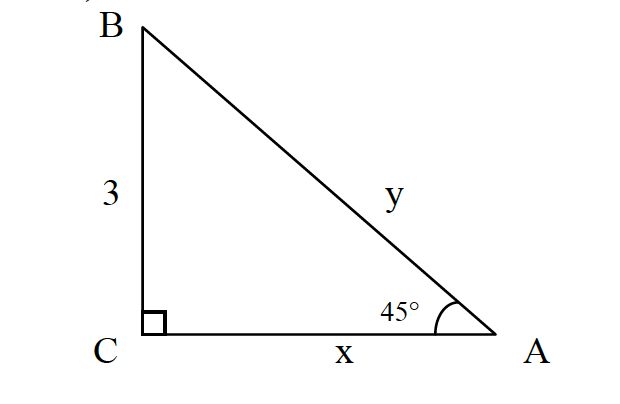
Show Answer 1
The triangle is a $45-45-90$ triangle. It is isosceles, so both legs measure the same. This means that $x=3$. The hypotenuse is
$$y=3\sqrt 2.$$
Try Question 2
Find $x$ and $y$. Leave the answer in simplest radical form.
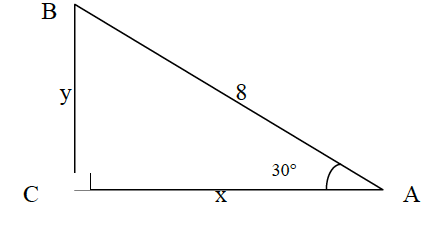
Show Answer 2
The triangle is a $30-60-90$ triangle. The hypotenuse has length $8$. The short leg is
$$y=\dfrac{8}{2}=4.$$
The long leg is
$$x=4\sqrt 3.$$
WeBWorK
You should now be ready to start working on the WeBWorK problems. Doing the homework is an essential part of learning. It will help you practice the lesson and reinforce your knowledge.
WeBWork
It is time to do the homework on WeBWork:
SpecialTriangles
TrigonometryRatios
When you are done, come back to this page for the Exit Questions.
Exit Questions
After doing the WeBWorK problems, come back to this page. The Exit Questions include vocabulary checking and conceptual questions. Knowing the vocabulary accurately is important for us to communicate. You will also find one last problem. All these questions will give you an idea as to whether or not you have mastered the material. Remember: the “Show Answer” tab is there for you to check your work!
Exit Questions
- What makes the 45-45-90 and the 30-60-90 triangles special?
- If the hypotenuse of the the 30-60-90 has length 2, what is the length of the side opposite 60?
- How many ratios are there? And what are they? How can they be written in terms of words like opposite, adjacent, and hypotenuse and must these terms be in relation to an angle?
$\bigstar$ Find $x$ and $y$. Leave the answer in simplest radical form.
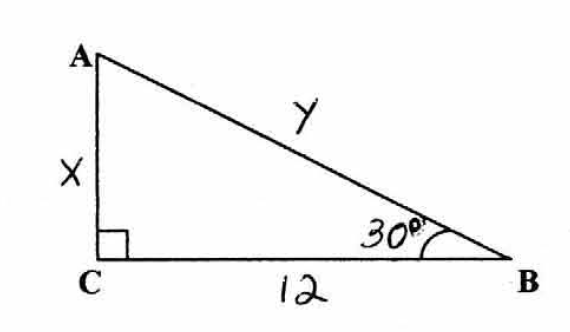
Show Answer
The triangle is a $30-69-90$ triangle. The long leg has length $12$. The short leg is
$$x=\dfrac{12}{\sqrt 3}=\dfrac{12\sqrt 3}{\sqrt 3\sqrt 3}=\dfrac{12\sqrt 3}{3}=4\sqrt 3.$$
The hypotenuse is twice the short leg
$$y=2\cdot 4\sqrt 3=8\sqrt 3.$$
Need more help?
Don’t wait too long to do the following.
- Watch the additional video resources.
- Talk to your instructor.
- Form a study group.
- Visit a tutor. For more information, check the tutoring page.



