Polynomials and their roots

Group activity: Give a definition of polynomial.

The idea of polynomials

Polynomials are the (smallest) collection of functions satisfying:

  • The constant functions and the identity function $f(x)=x$ are polynomials.
  • If you combine two polynomials using the operations addition, subtraction, or multiplication, then the result is a polynomial.

The definition of polynomials

Definition: a polynomial function is any function of the form $f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ for fixed numbers $a_{n}, \ldots, a_{0}$ $\left(a_{n} \neq 0\right)$ and $n$ is called its degree.

Group activity:

  • What do the following terms mean with regards to polynomials?
    • degree
    • root
    • factor
  • Describe any connections between these three terms.

Pre-discussion poll of the class

  • Can all polynomials be factored?
  • Does every polynomial have a root?
  • If a polynomial has a root at $x=2$, does the graph of the polynomial cross the x-axis at $x=2$?
  • If a polynomial has a factor, does it have a root?
  • If a polynomial has a root, does it have a factor?
  • Is it possible to factor a polynomial that has no root?
  • A polynomial of degree n has _______ roots.

Examples. Look at the graph of each polynomial. How many roots does it have? Does it factor?

  • $f(x)=x^2-5x+6$ (2 factors, 2 roots)
  • $g(x)=x^2-3x+4$ (no factors, no roots)
  • $h(x)=x^3-9x^2+27x-27$ (3 factors, 1 root)
  • $j(x)=x^3-x$ (3 factors, 3 roots)
  • $k(x)=x^4+3x^2+2$ (2 quadratic factors, no roots)

Theorem. If a polynomial $f(x)$ has a root $r$, then $f(x)$ can be written in the form $f(x)=(x-r)\cdot q(x)$, where $q(x)$ has degree one less than the degree of $f(x)$.

What does this theorem allow us to say about the roots of a polynomial $f(x)$ of degree 4? Discuss

Theorem. Every polynomial can be factored into a product of linear and irreducible quadratic factors.

Multiplicity and the shape of the graph near a root

Definition. The multiplicity of a root $x=r$ in a polynomial is the number of times that the linear factor $(x-r)$ appears in the complete factorization of that polynomial.

Shape of the graph near a root. If a polynomial has a root at $x=r$, the behavior of the graph near $r$ always fits one of these descriptions:

  1. The graph passes through the x-axis at $x=r$ without leveling off.
  2. The graph levels off until it is tangent to the x-axis at $x=r$. It touches but does not cross the x-axis there.
  3. The graph levels off until it is tangent to the x-axis at $x=r$, and crosses the x=axis there.

Exercise: For each polynomial, what are the roots? What is the multiplicity of each root? What is the shape of the graph near the root?

  • $f(x)=x$
  • $g(x)=x^2$
  • $h(x)=x^3$
  • $j(x)=x-1$
  • $k(x)=(x-2)^4$
  • $m(x)=(x-3)^7$

Exercise. For each polynomial, what are the roots? What is the multiplicity of each root? What is the shape of the graph near the root?

  • $h(x)=x^3-1$
  • $f(x)=x^5(x^2+2x+1)(x^2+2x+6)$
  • $g(x)=(x-5)(x+2)(x-6)(x+2)(x-6)(x-5)(x-6)(x+2)$

Question: What is the connection between the multiplicity of a root and the behavior the graph near that root?

Exercise. Guess the formula for each polynomial. You may use Desmos or another graphing utility.

a.

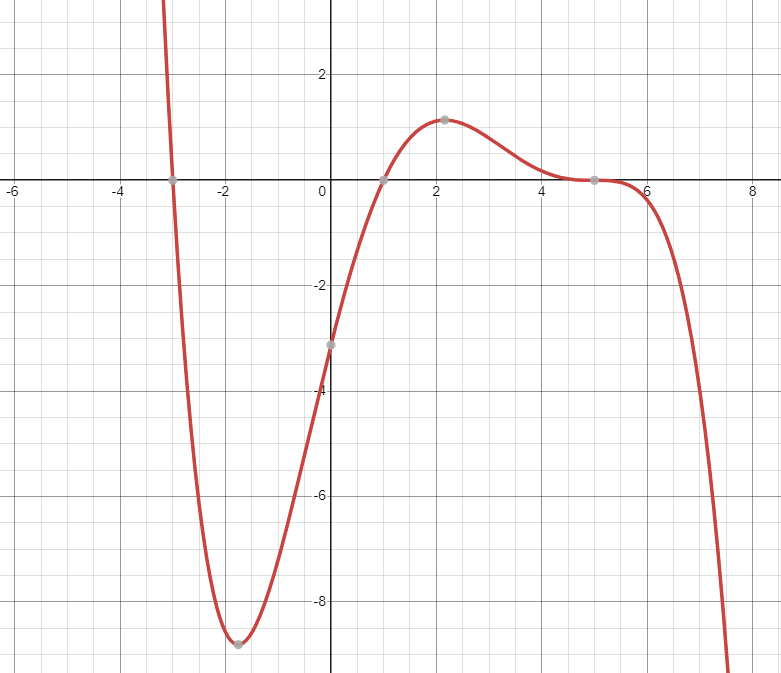
Polynomial with roots at -3, 1, and 5

b.

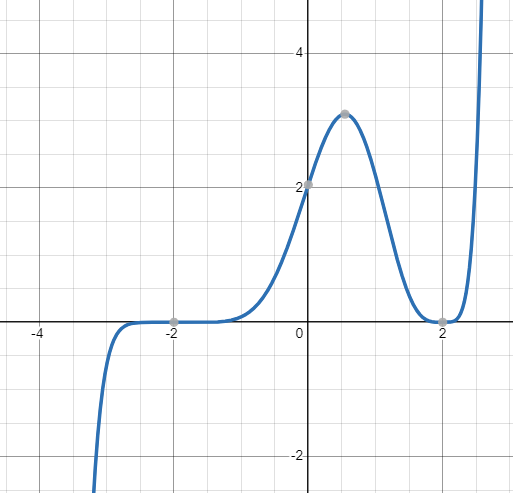
Polynomial with roots at 2, -2

c.

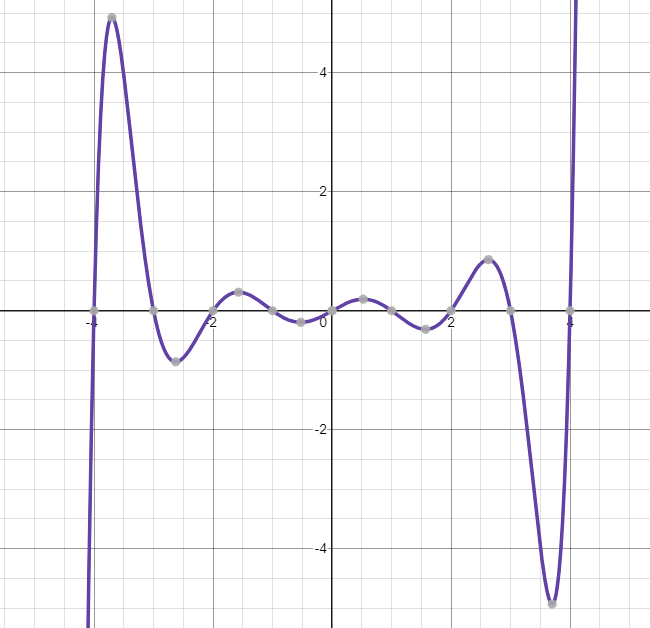
Polynomial with roots at -4, ..., 4

d.

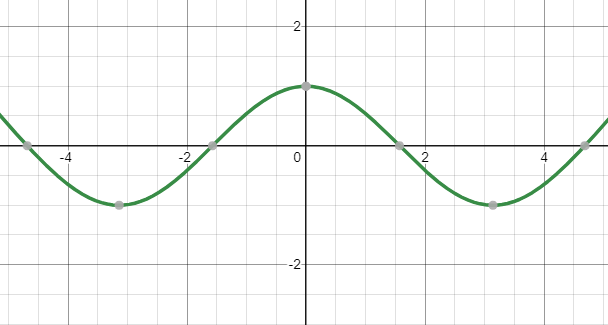
Polynomial approximating cosine x

Theorem. If a polynomial $f(x)$ has odd degree, then it has at least one root.

Theorem. The end behavior (the limit as approaches infinity or -infinity) of a polynomial is the same as that of the leading term $a_nx^n$.

Resource: For a more detailed exposition of this material, here is a page about Polynomials and their graphs on the MAT 1375 Course Hub (it includes a great video with examples of finding polynomials to match polynomial descriptions, created by past City Tech MEDU student Irania Vasquez)