Hi everyone! Read through the material below, watch the videos, and follow up with your instructor if you have questions.

Lesson 9: Graphing polynomials

Topic. This lesson covers Session 9: Graphing polynomials

Learning Outcomes.

  • Make connections between geometric features of polynomials (roots, extrema, end behavior) and corresponding algebraic features (factors, coefficients, etc).
  • Translate between graphs, formulas, and natural language descriptions of polynomials.

WeBWorK. There is one WeBWorK assignment on today’s material:

  1. Polynomials – Graphs

Additional Video Resources.

Question of the Day: How can we find the formula for function by looking at the graph?

Graphing Polynomials

In this lesson, we will explore the connections between the graphs of polynomial functions and their formulas. By the end of the lesson, you should be able to:

a) Look at the graph of a polynomial, estimate the roots and their multiplicities, identify extrema, and the degree of the polynomial, and make a guess at the formula.

b) Look at the formula of a polynomial and determine the roots and end behavior.

c) Write a formula for a polynomial meeting certain conditions (i.e. with certain roots, end behavior, etc.)

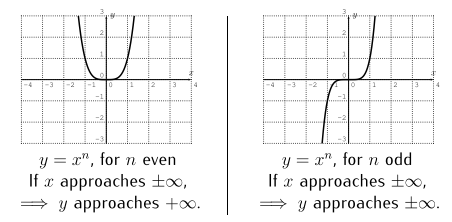
Graphs of functions $f(x)=x^n$

Consider the graphs of the functions $y=x^n$ for different values of $n$:

Graphs of x^2, x^3, x^4, x^5

From the graphs, you can see that the overall shape of the function depends on whether $n$ is even or odd.

If n is even, the graph of y=x^n goes up (y approaches infinity) both to the left (as x approaches negative infinity) and the right (as x approaches positive infinity). If n is odd, then the graph goes up to the right, but down to the left.

Graphs of polynomials of degree 2

Observation. Let $f(x)=a x^{2}+b x+c$ be a polynomial of degree $2$. The graph of $f$ is a parabola.

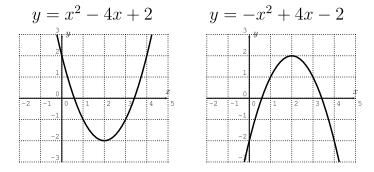
Graphs of y=x^2-4x+2 and y=-x^2+4x-2.
  • $f$ will have at most two roots.
  • $f$ will have a single extrema (maximum or minimum, “turning point”)
  • If $a>0$ ($a$ is the number in front of the $x^2$) then $f$ opens upwards, if $a<0$ then $f$ opens downwards.

Graphs of polynomials of degree 3

Observation. Let $f(x)=a x^{3}+b x^{2}+c x+d$ be a polynomial of degree 3.

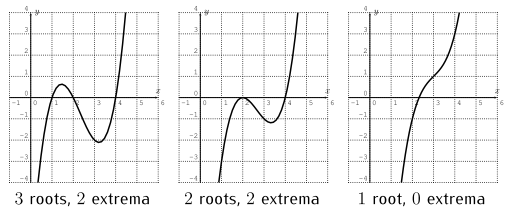
Graphs of three cubic functions with various combinations of roots and extrema.
  • The graph may change its direction at most twice ($f$ will have at most two extrema).
  • $f$ will have at most 3 roots.
  • If $a>0$, then the graph goes up to the right, down to the left. If $a<0$ then the graph goes down to the right, up to the left.

Graphs of polynomials of any degree

Observation. Let $f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{2} x^{2}+a_{1} x+a_{0}$ be a polynomial of degree $n$.

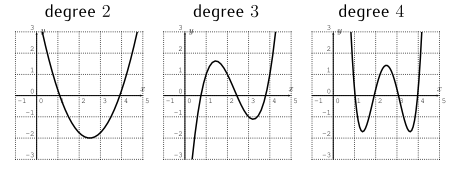
Graphs of polynomials of degree 2, degree 3, and degree 4
  • Then $f$ has at most $n$ roots, and at most $n-1$ extrema.
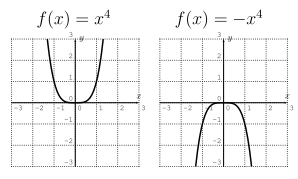
Graphs of f(x)=x^4 and f(x)=-x^4
  • If the degree of $f$ is even, $n=2,4,6,\dots$: If the leading coefficient $a_n >0$ then the graph opens upwards, if the leading coefficient $a_n < 0$ then the graph opens downwards.
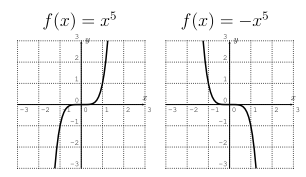
Graphs of f(x)=x^5 and f(x)=-x^5
  • If the degree of $f$ is odd: If the leading coefficient $a_n>0$, then the graph of $f$ goes up to the right, down to the left. If the leading coefficient $a_n<0$, then the graph of $f$ goes down to the right, up to the left.

Example. Find a function $f(x)$ of degree 3 with roots $x=6$ and $x=-4,$ where the root at $x=-4$ has multiplicity two.

Example. Determine the polynomial function $f(x)$ with leading coefficient $-2,$ of degree $3,$ and having roots $x=2$, $x=-2-5 i,$ and $x=-2+5 i$. Your final answer should not contain any $i$ ‘s.

VIDEO: Finding polynomials to match polynomial descriptions

Video by Irania Vazquez

Exit Question

Example. Without using a calculator, match each graph to its formula:

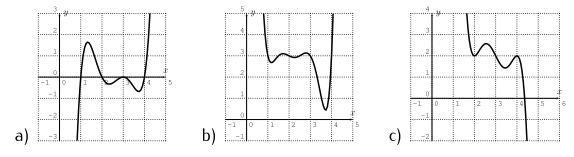
Graphs of three polynomial functions

i) $\quad f(x)=x^{6}-14 x^{5}+78.76 x^{4}-227.5 x^{3}+355.25 x^{2}-283.5 x+93$
ii) $\quad f(x)=-2 x^{5}+30 x^{4}-176 x^{3}+504 x^{2}-704 x+386$
iii) $\quad f(x)=x^{5}-13 x^{4}+65 x^{3}-155 x^{2}+174 x-72$

Answer

Notice that graph a) goes up to the right and down to the left. From this we conclude that the function has odd degree, and also must have a positive leading coefficient. The only answer that fits these criteria is iii).

Graph b) must have even degree and a positive leading coefficient, so b) fits with i).

Graph c) has odd degree but must have a negative leading coefficient (since it goes down to the right and up to the left), which confirms that c) is ii).

Answer: a)-iii), b)-i), c)-ii)