Categorical vs quantitative variables

Quantitative variables are any variables where the data represent amounts.
Categorical variables are any variables where the data represent groups.

Example

Survey 100 students, record:

  • height
  • gender
  • hair color
  • age

Which variables are categorical? Which are quantitative?

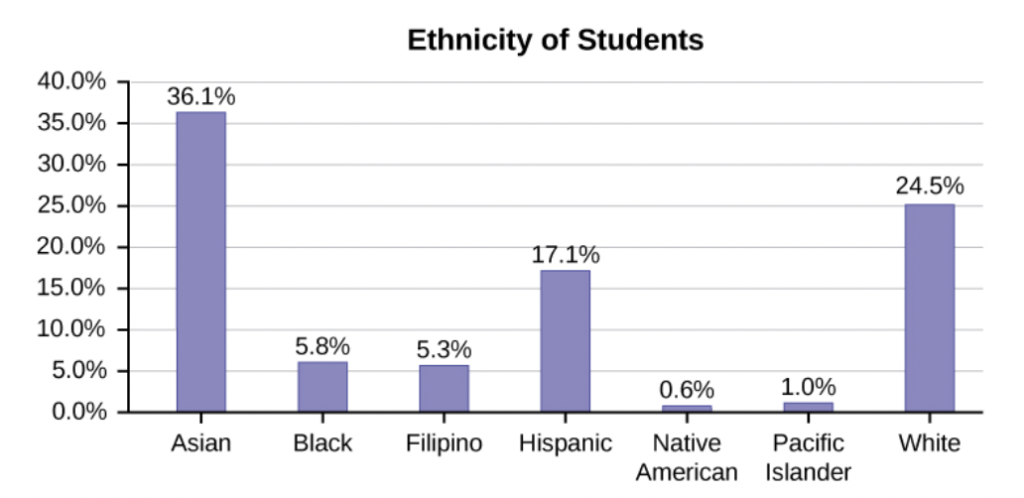
Typical question: What is the probability that a randomly selected student is Filipino?

Height of Students (ft)

Typical question: What is the probability that a randomly selected student is between 5 and 6 feet?

The normal distribution

Cool and handy fact: An enormous number of different kinds of continuous real-world variables have the same shape – the bell curve (or normal distribution).

The normal distribution

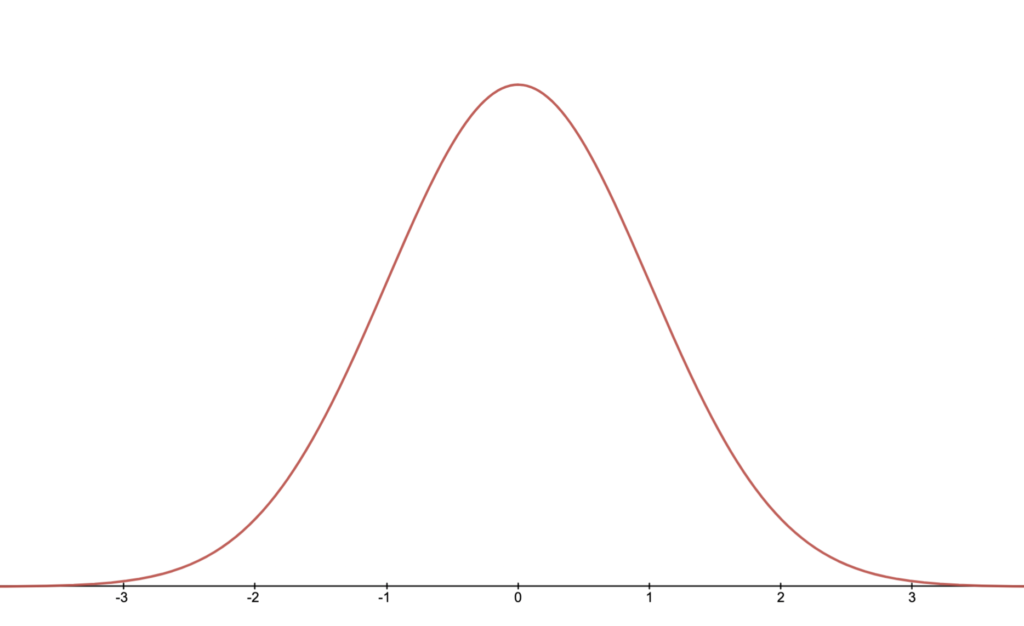
This curve is based on the function y=e^{-x^2}, with constants added in appropriate places to make the values work out correctly (total area = 1, inflection points at +-1, and so on).

The normal distribution with mean \mu=0 and standard deviation \sigma=1 (this is the “basic” normal distribution – we often use z as a variable to set it apart): f(z)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}z^2.

Normal distributions with different mean and standard deviation

What if our random variable is measuring height? Then the mean will not be \mu=0 ft — it’s more likely the mean will be something like \mu=5.8ft. And the standard deviation may not turn out to be \sigma=1.

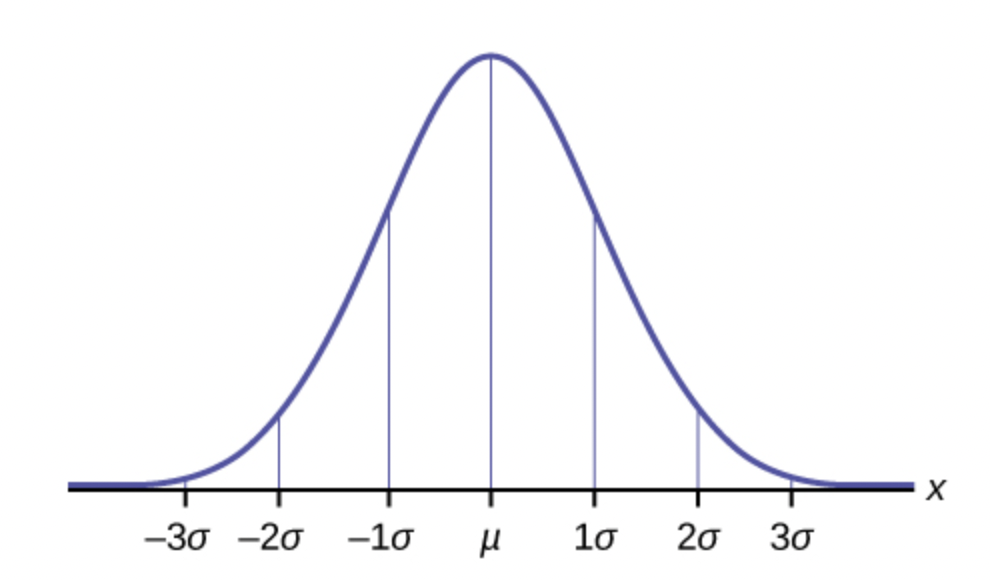
Normal Distribution

The normal distribution with mean \mu and standard deviation \sigma: f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{2}}.

Example 1

How do we actually calculate probabilities using the normal distribution?

Option 1. For certain simple values, use the 68-95-99.7 rule.

Option 2. Use the TI-84+ calculator.

  • Press 2nd Distr
  • Press 2:normalcdf(lower bound, upper bound, mean, standard deviation)
  • Example: normalcdf(-1000,-64.9,79,7)

Option 3. Use the formula. In particular, calculate the area under the normal distribution curve f(x) from the left bound to the right bound.

    \[\int_a^b \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{2}} dx\]

What is the 68-95-99.7 rule?

  1. About 68% of values fall within one standard deviation of the mean.
  2. About 95% of the values fall within two standard deviations from the mean.
  3. Almost all of the values—about 99.7%—fall within three standard deviations from the mean.
The normal distribution, and standard deviation with the confidence level. | Download Scientific Diagram

Example 2

Example 3

Example 4

Resources on Probability and Statistics