Before we can discuss volume, we have to know some basic facts about 3- dimensional space. The first order of business is to set up a coordinate system in 3-space. To this end, we want three lines passing through a point O so that they are mutually perpendicular.

Wu, PCC
3D coordinate axes demonstrating the right-hand rule.
The right-hand rule

Just as in the case of 2 dimensions, “congruence” in 3 dimensions is based on isometries, or distance-preserving maps. Every isometry is a combination of the three basic isometries.

Basic Isometries in 3 Dimensions

  1. Rotation of $r$ degrees around a line.
  2. Translation by $(a,b,c)$.
  3. Reflection across a plane.

Distance formula in 3D

The distance between two points $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ is given by $\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}$

Cavalieri’s principle

If two solids are placed between two parallel planes and if the areas of the two planar regions cut out in the solids by any plane parallel to the top and bottom planes are always equal, then the volumes of the two solids are also equal.

Cylinders

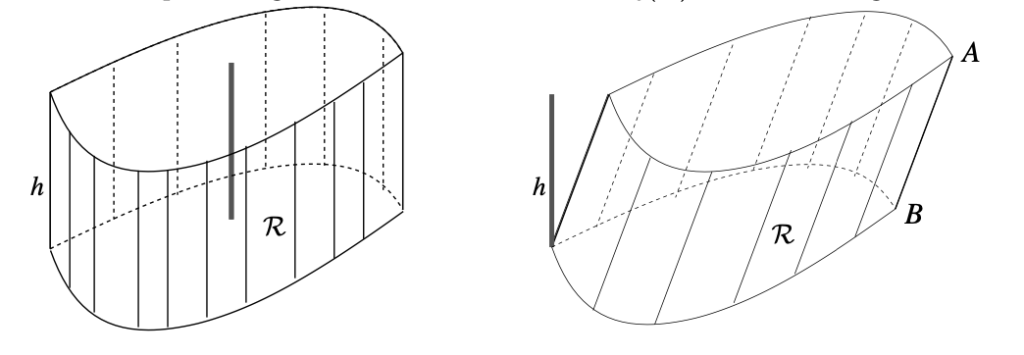
Right cylinder of height h over a region R, Cylinder of height h over a region R.
Right cylinder of height h over a region R, Cylinder of height h over a region R.

The volume of a cylinder is given by $|R|*h$, where $|R|$ is the area of the base and $h$ is the height (distance between top and bottom

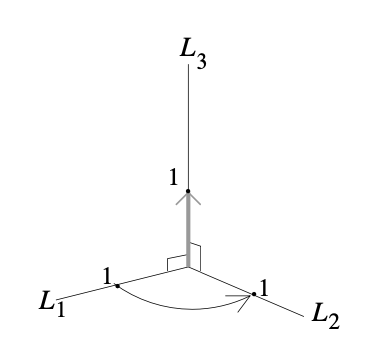
Cones

If $R$ is a region of a plane and $P$ is a point not on the plane containing $R$, then the union of all the segments joining the point $P$ to a point in the base $R$ is called a cone with base $R$ and vertex $P$. The height h of the cone is the distance from $P$ to the plane containing $R$.

  • If $R$ is a circle then the cone is called a circular cone. If, in addition, the vertex is located on the line perpendicular to the circular base at its center, then we call is a right circular cone.
  • If $R$ is a square we call the cone a pyramid.

The volume of a cone with base $R$ and height $h$ is $\frac{1}{3}\cdot(\text{volume of cylinder with same base and same height})$.

The volume of a sphere with radius $r$ is $V=\frac{4}{3}\pi r^3$