Very roughly, a geometric measurement (i.e. length, area, and volume) assigns a nonnegative number to a geometric figure that serves to indicate the “size” of the figure relative to a particular chosen unit of measurement.
Wu, PCC
The idea of measurement is fundamental, and grounded in our daily experience of length, area and volume. It is therefore somewhat surprising that the mathematical underpinnings of measurement are quite deep and are often not fully explored until a course in real analysis.
While the concepts of length, area, and volume give the appearance of being straightforward and intuitive, they are inherently complex.
Wu, PCC
While we can intuitively measure certain simple figures (lengths of line segments, areas of rectangles, volumes of rectangular solids), extending these notions to more general figures requires the use of the limits. Even with this powerful tool in mind, there will always be some examples of figures that we cannot assign a numerical value to in a coherent fashion – so-called unmeasurable sets.
Finally, although we are comfortable with different kinds of measurement for different types of figures (length, area, and volume), it’s not always clear that these three kinds of measurement are, at heart, the same – they are all governed by four basic principles, M1-M4.
Notationally, we will use $G$ to refer to a figure (so $G$ could be a line segment, or a curve, or a rectangle, or a sphere, etc.). We will denote the measure of a figure $G$ by absolute value signs, $|G|$.
Properties of measurement
(M1) There is a fixed figure called the unit figure with measure 1
- the unit interval, the unit square, the unit cube
(M2) Congruent figures have equal measure.
(M3) (Additivity). If $G_1$ and $G_2$ are figures that overlap only on their boundaries, then the measure $|G_1 \cup G_2| = |G_1|+|G_2|$
- for example: two curves that meet at a common endpoint, two rectangles that share a side, two cubes that share a face
(M4) (Limits). If we have a sequence $\{G_n\}$ of figures that converges to a figure $G$ then the measure of $G$ is the limit of the measures of $G_n$.
- defining the idea of convergence of geometric figures in this scenario requires some care – however, for our purposes the intuitive notion that the figures $G_n$ are getting “closer and closer” to the figure $G$ will suffice.
How do we define the length of a curve?
- unit interval
- lengths of line segments
- lengths of curves
How do we define the area of a shape?
- unit square
- areas of rectangles
- areas of more general figures
How do we define the volume of a solid?
- unit cube
- volumes of rectangular solids
- volumes in general
Area of a shape
Start with a shape $R$ in the plane.
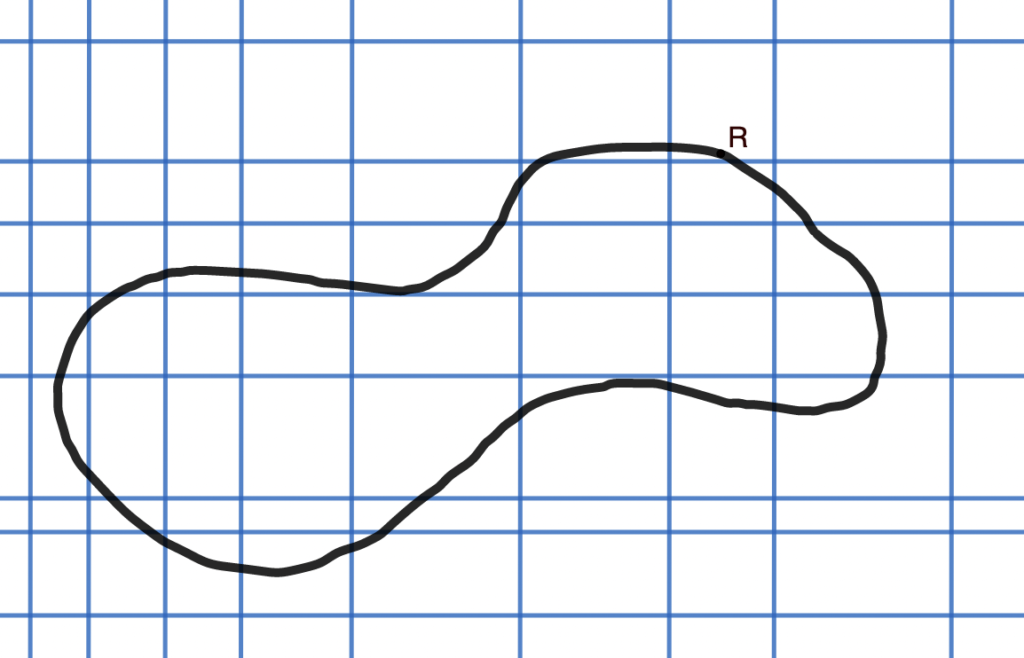
Add a finite number of horizontal and vertical lines to create a grid.
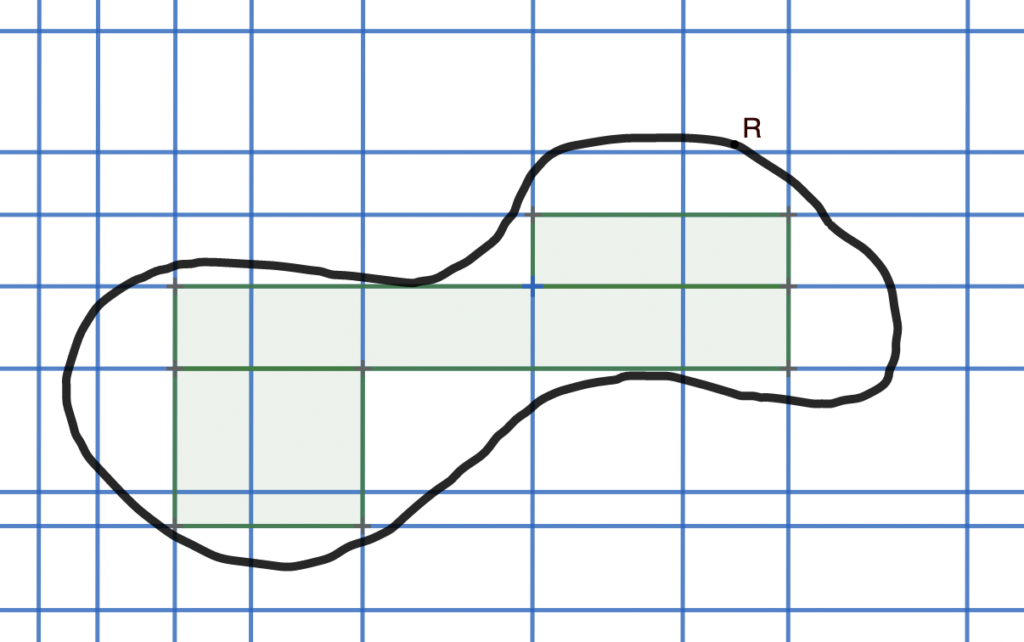
To get an underestimate of the area, color in all rectangles that are entirely contained within $R$ (green). We know how to calculate the area of a rectangle, so we can add up the areas of all the green rectangles.
To get an overestimate of the area, color in all rectangles that contain any part of $R$ (yellow).
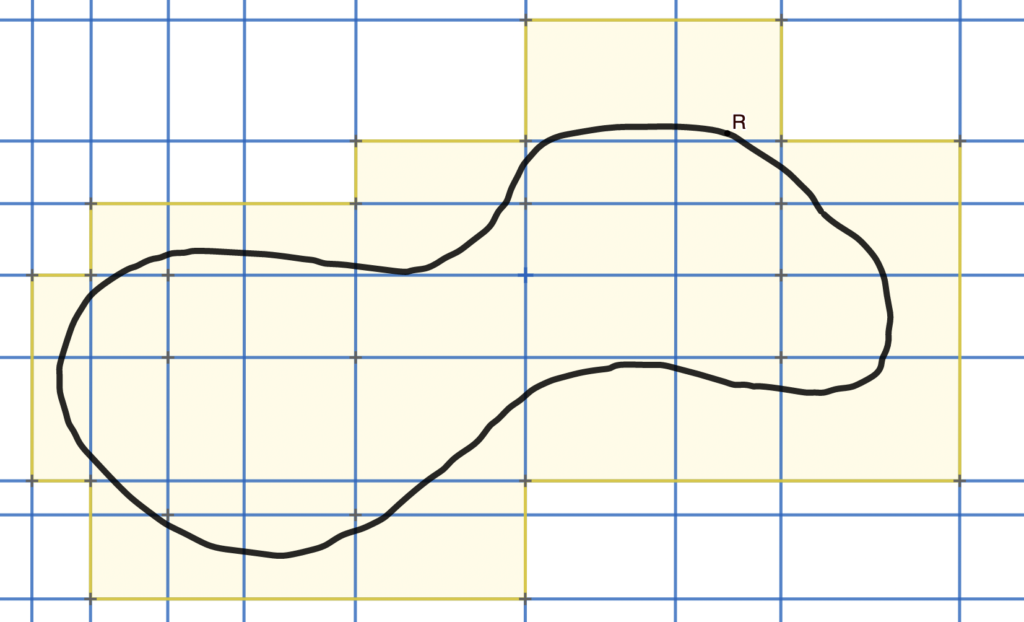
How can we improve these estimates?



0 Comments
1 Pingback