Circles arise naturally in geometry (they are an immediate consequence of the notion of distance), and we use them extensively in geometric constructions (after all, a compass is essentially a “circle-drawing tool”). However, we focus much more on proving facts about triangles, and figures involving triangles. What can be said about circles themselves?
Circle
Definition. Given a point $P$ and a positive real number $r$, the circle with center $P$ and radius $r$ consists of all points in the plane of distance $r$ from $P$.
Circles and Line Segments
A diameter of a circle is any line segment with both endpoints on the circle which passes through the center $P$. Note: Sometimes we use the word “diameter” to mean the length of such a segment.
A radius of a circle is any line segment with one endpoint at the center $P$ and the other endpoint on the circle. NOTE: Once again, we sometimes use the word “radius” to mean the length of such a segment.
Chords and Arcs
A chord of a circle is any line segment with both endpoints on the circle.
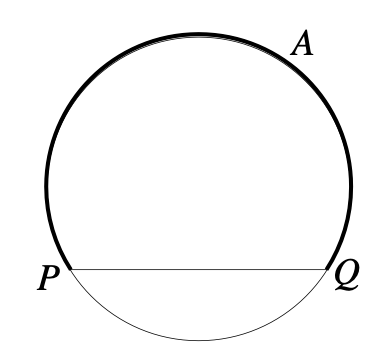
Arc. If $P$ and $Q$ are distinct points on a circle, then we can imagine the chord $\overline{PQ}$ dividing the circle into two parts, called arcs. When we use the notation $\stackrel{\frown}{PQ}$ it is usually clear from context which of these two arcs we mean – but sometimes, an additional letter is provided to help the reader.
Example: In the image below $\stackrel{\frown}{PAQ}$ refers to the upper arc.
Drawing angles in circles
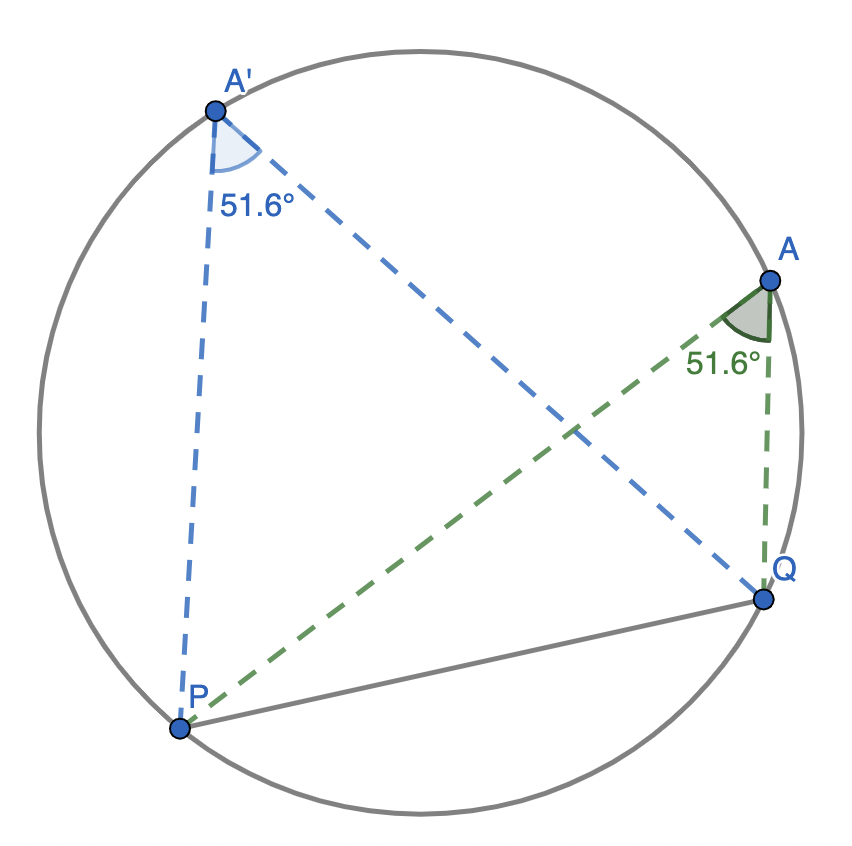
What if we use a different chord (not a diameter)?
Theorem. If $\overline{PQ}$ is a chord of a circle and $A$ is any other point on the circle, then the measure of $\angle{PAQ}$ does not depend on the choice of $A$ – we call this the angle subtended by $\stackrel{\frown}{PQ}$.
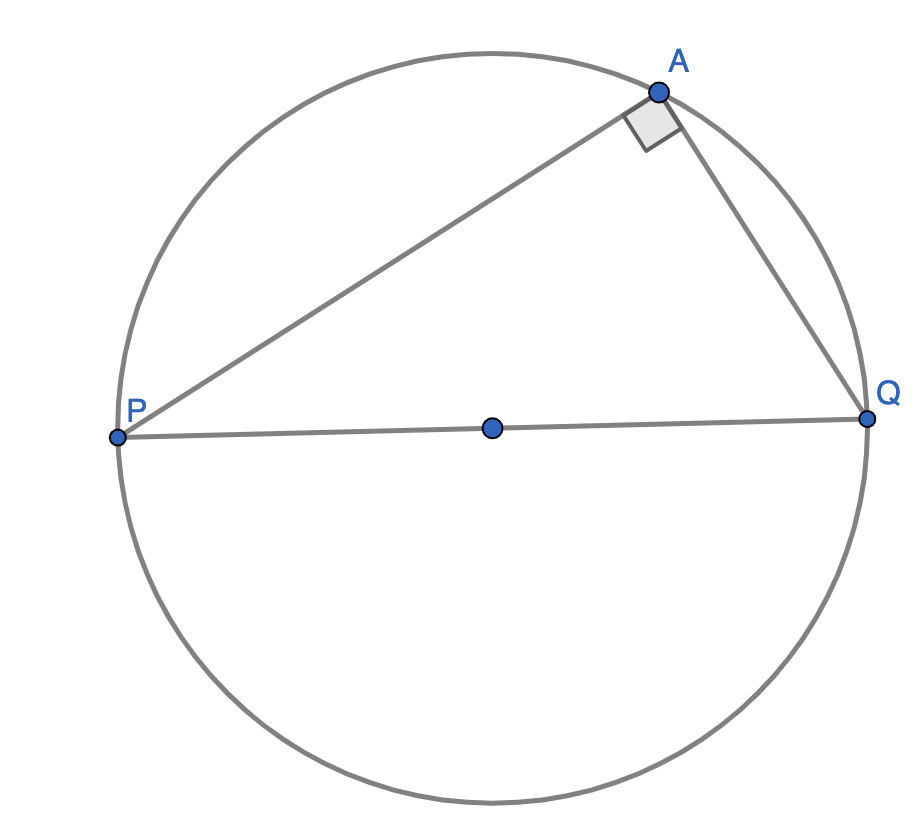
This angle is $90^\circ$ if and only if the chord $\overline{PQ}$ is a diameter.
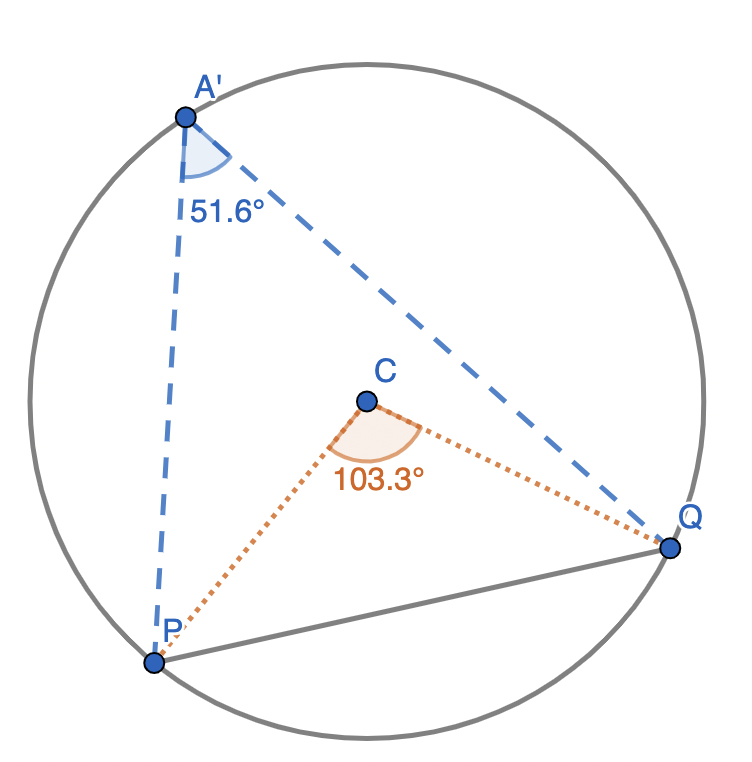
Finally, what if we consider angles with vertex at the center of the circle (instead of on the circle itself)?



0 Comments
1 Pingback