How do we define the slope of a line?
The coordinate plane
The coordinate plane, labelling each point in the plane with a pair of numbers (coordinates), allows us to understand geometric objects in terms of algebra, and algebraic objects in terms of geometry.
Definition of slope
The idea that we can associate a single number, called slope, with a line in order to capture the line’s steepness is a subtle one. In TSM, the slope is usually defined as “rise over run,” with a corresponding formula $\frac{y_2 – y_1}{x_2-x_1}$ for calculating slope based on the coordinates of any two points on the line. However, it’s not clear at the outset that slope is well-defined notion – in particular, how do we know that if we choose different points, we will get the same result? This needs to be proved! How do we give an underlying definition, something simple that we can fall back on? We can then prove that the formula above works to calculate the slope given in our definition?
We’ll define slope in a few stages. First, let’s consider lines passing through the origin (we will set aside vertical lines for the moment).
Local slope at the origin O
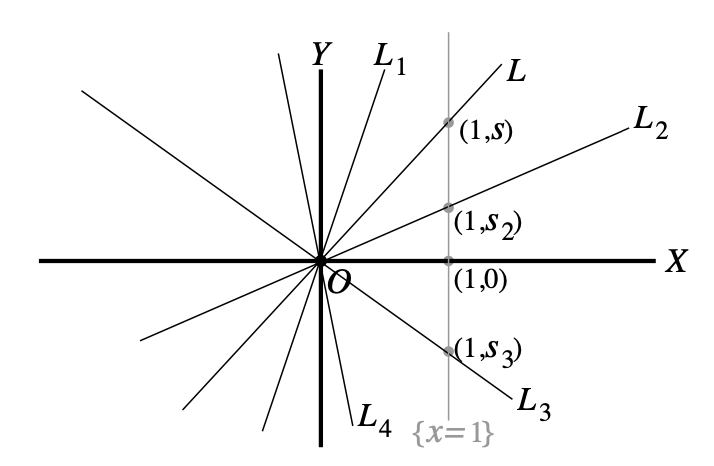
Definition. Let O be the origin $(0,0)$. Suppose $L$ is a nonvertical line passing through O. Then $L$ intersects the vertical line $x=1$ in one point $(1,s)$. We call $s$ the local slope of $L$ at O.
Local slope at a point P
Definition. Let $P$ be a point with coordinates $(x_0,y_0)$. Suppose $L$ is a nonvertical line passing through $P$. Then $L$ intersects the vertical line $x=x_0+1$ in one point $(x_0+1,y_0+s)$. We call $s$ the local slope of $L$ at $P$.
Local slope is the same everywhere
LEMMA 6.7. The local slope of a nonvertical line $L$ at $P$ for a point $P \in L$ does not depend on $P$.
Slope
Definition. Let $L$ be a nonvertical line in the plane. The slope of $L$ is the local slope of $L$ at $P$ for any point $P$ on $L$.
Formula for slope
THEOREM 6.10. On a given nonvertical line $L$, let any two distinct points $P_{1}=\left(x_{1}, y_{1}\right)$ and $P_{2}=\left(x_{2}, y_{2}\right)$ be chosen. Then the slope of $L$ is equal to the ratio
$$
\frac{y_{2}-y_{1}}{x_{2}-x_{1}}
$$
This ratio is also called the difference quotient of $P_1$ and $P_2$.



0 Comments
2 Pingbacks