Kids love to ask “Why?”
If you’re like most people who attended public school in the U.S., most of the math you’ve done in your life has been primarily computational, or algorithmic – you learn a kind of problem, you learn a method to solve it, you practice it a few times, and you demonstrate that you’ve learned it by solving a problem on an exam. Maybe the solution involves memorizing a formula, or a set of steps (an algorithm). Very seldom are you asked to consider the reasons behind the method – what I call the “why” questions. And if you ever asked these kind of questions, there is a good chance that you were not often given a very satisfying answer.
Questions you may not have spent much time on in math class:
- Why does the formula look like this, instead of something else?
- Why do we do these steps, in this order? How do we know this method actually works? Why does it work?
- Why is this fact (“theorem”) true? I don’t believe it – can you convince me?
- What’s the big deal about this fact (or formula)? Why is it important?
To begin this assignment, I’d like you to spend some time thinking about the different kinds of math you’ve learned in your life. Look at math textbooks or class notes from past and current classes. Think about the math skills you learned at different ages – from early experiences with counting, up through things like algebra or geometry, and on to Calculus or Linear Algebra or other recent courses. If you still have some old math work from your high school, middle school, or elementary school years that might help too (maybe your parents kept some of your childhood work?). If you’re in the Math Ed program, you can think about the math that you are working on in your MEDU courses. As you consider these topics, think about the “why” questions – when you were learning this topic, did you spend time in class talking about “why?” Did you do activities or other work that helped you understand the reasons for the formulas and methods that you learned?
Assignment (due Thursday 10/2/14). The assignment consists of two parts. Be sure to answer each part completely (they are equally important).
1. Describe a time that you DID learn about the “why” behind a mathematical idea (why something works, or where it came from, etc.). Tell us about it – how old were you, what was the class (or did it happen outside of class?), what was the topic, and what did you learn?
One example that came up in a class discussion was the activity introducing the number 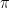 by having students measure the diameter and circumference of various circular objects, and showing that the ratio was always a little more than 3.
by having students measure the diameter and circumference of various circular objects, and showing that the ratio was always a little more than 3.
2. State three questions about math that you do not know the answer to (but would like to!). For each question, tell us why you find it interesting. The questions…
- …should involve “why” or “how”
- …should be about math topics that you are already familiar with – things you’ve studied (you need not be an expert)
- …should come from different math topics, at different levels (some examples: arithmetic, fractions, algebra, geometry, functions, calculus, probability, … )
Some examples of “why” questions.
- Why does
 equal
equal 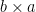 ?
?
- Why do we need a common denominator when we add fractions?
- How do we know that
 is irrational (not equal to a fraction)?
is irrational (not equal to a fraction)?
- Where does the quadratic formula come from? How do we know it always works?
- The fundamental theorem of calculus gives us a way to evaluate an integral – for example, to find the area under a curve. How do we know this actually works, and gives the correct answer?



