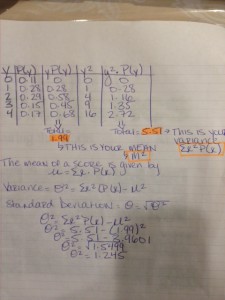
Jonathan likes to play soccer. Assume y=number of goals that Jonathan has scored during the fall season and assume y can only take values from 0 to 4. The following table represents the probability distribution for the discrete random variable y.

When given this sort of problem we usually start with the two first rows which are x and p(x) (In this case we are using a y instead of x)

The first row Y has the numbers 0,1,2,3,and 4.

The second row P(Y) is given as 0.11, 0.28, 0.29, 0.15, and 0.17

We then have to create the last three rows which are always in the following order as Y*P*Y, then Y2, and lastly Y2*P*Y

The third row Y*P*Y is basically the first two rows multiplied together 0*0.11=0 , 1*0.28=0.28, 2*0.29=0.58 and so on.

The fourth row Y2 is simply squaring the first row which gives us 0,1,4, 9 and 16

The last row is the Y2 row multiplied with the original P(Y) row. 0*0.11=0, 1*0.28=0.28, 4*0.29= 1.16, 9*0.15=1.35 and so on. ( this is the part where one should be careful to multiply the original P(Y) with the Y2 and not Y*P*Y because all the rows are close together. This is a mistake that can be easily made so its always a good idea to double check your work quickly before continuing with the rest of the problem.)

You can see the finished chart in the picture posted above.

Question A then asks us to find the probability that Jonathan would score exactly 3 goals in the fall season. In the orginal problem under the number 3 that number is blank and we are left to figure that out. The simpliest way to explain that is that the sum of all probabilities must equal 1, since we know this we can take all the given numbers that are listed under P(Y) and add them up which gives us 0.85. When you subtract the sum of 1.00 from 0.85 that gives us 0.15 which you then fill in the blank with to add up to 1.

That answers the question what is the probability that Jonathan scored exactly 3 goals= 0.15

Question B asks the probability that Jonathan would score at least 2 goals in the fall season. We know that when we see the pharse “at least” it means that and more such as “at least 21 meaning 21 or older. In this case we add 0.29+0.15+0.17= 0.61

The answer is Jonathan has a 0.61 probability of scoring at least 2 goals.

Question C is to find the mean of the probability distribution. When you want to find the mean you look at the row Y*P*Y you add up all those probabilities and that gives us a total of 1.99.

Question D we have to find the standard deviation of the probability distribution. When doing this part its actually two quick steps. You look at your last row X2*P*X and add those  up and we get a total of 5.51.

We then use the formula for variance and plug in the standard deviation and the mean squared which is worked out in the picture above:

**Remember to use the order of operations when doing this formula. We square the 1.99 first and then subtract the 5.51 from the 3.901 which gives us 1.5499. We the take the square root of that which gives us 1.245.