Make a translation puzzle (Due Thursday, October 3). Your assignment this week is to take a common phrase – a saying, a quote, a song lyric, or anything recognizable to most people – and translate it into logical notation. You should break it up into individual parts (such as P, Q and R), and then combine them using logical notation to create your phrase. This is meant to be a puzzle for your classmates, so do NOT include the original phrase.
Your submission should include: the individual parts P, Q, R etc. (written in English), and the puzzle itself (written in logical notation).
Extra Credit. You can earn extra credit by responding to a classmate’s puzzle – either by being the first person to correctly guess the phrase, or by making suggestions, or by offering an alternative way of translating the phrase into logical notation.
Here are two examples:
1.
P: you're happy
Q: you know it
R: clap your hands
Puzzle: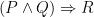 
Answer: “If you’re happy and you know it, clap your hands”
2.
P(x,y): you can fool person x at time y
Puzzle: 
Answer: “You can’t fool all the people all the time”
How do I type logical notation on the OpenLab? This is not too hard — BUT it takes a little getting used to. Here’s an example. If you type this into a comment:
Here is a statement: $latex P \wedge Q $
then (after you post the comment) you should see this:
Here is a statement: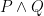 
Each equation or expression begins with “$latex ” and ends with “$”. In between “$latex ” and “$” you type your math — many things you type just as they are, like letters and numbers, but each special symbol has a special code. In the example above, we use the code “\wedge” to produce the upside-down vee which means “and”.
Here are a few more examples:
| Type this: |
to get this result: |
| $latex P \vee Q$ |
 |
| $latex P \Rightarrow Q$ |
 |
| $latex \sim P$ |
 |
| $latex \bar{P}$ |
 |
| $latex P \Leftrightarrow Q$ |
 |
| $latex \forall x, P(x)$ |
 |
| $latex \exists x, P(x)$ |
 |
| $latex \forall x \exists y ( P(x) \vee Q(y)) \implies R(x,y) $ |
 |
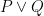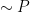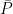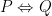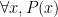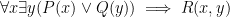LaTeX tester. Want to test out your LaTeX code before you post it in a comment? There is a LaTeX tester here, where you can type in your formula, hit the button, and see how it looks: http://samples.geekality.net/latex/.
NOTE: When you use the test, do NOT include the dollar signs or the word “latex” — just include the stuff in between.
Finally, if you submit a comment but you find it doesn’t look right, don’t hesitate to make corrections and submit it again – you will NOT be penalized for multiple submissions!
