OpenLab Assignment (Due next Tuesday evening, March 16th). Your second exam will take place next week. The review sheet and answer key have been posted. In the interest of making this assignment a help (instead of an extra chore), I’m asking you to post a comment related to the second exam. Any one of the following types of comments will earn you full points:
- A request for help on a question. It must be more specific than just “how do I do this problem?” Let us know where you’re stuck (and what you’ve done so far). If you don’t know how to get started on a problem, you can say so — but tell us a little about why (is it different from problems we did in class?). Your post must use correct
notation!
- A general question about a topic that we’ve been studying. Is there some part of the course that’s been bothering you? A type of problem that you just don’t get? Something you keep trying but always get wrong? Post a question here – maybe someone can help.
- An answer to someone else’s question. You don’t have to give every step or every detail, but you should provide enough information to help them along. Your post must use correct
- A helpful comment or suggestion about a topic that we’ve been studying. Do you have a trick for solving certain problems? A neat way of remembering a formula? Some thoughts about what makes certain problems hard, and suggestions for solving them? Post it!
WeBWorK Update: As you all know, WeBWorK access has been terrible this week! Our hardworking system administrator is trying to figure out what’s going wrong, but until the difficulties get worked out I am making the following changes:
- WeBWorK assignment #1 will be extended for 2 weeks, and is now due on March 20th (this update will be made on the WeBWorK servers as soon as I can get access to them…).
- There will be no new WeBWork assigned until the current difficulties are resolved. We’ll pick up again once the system is working more reliably.
- Some of you may have noticed Assignment #2 in the WeBWorK system. This will be removed shortly — you don’t have to worry about it.
I hope this addresses your concerns about our current WeBWorK problems!
I don’t understand how to integrate
from problem 2
There have been a number of questions about this (see below). debitcard has it almost right in his response below — first, simplify the function to obtain:
next, use a substitution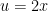
.
(note: since the real complication here is the “2” in front of the “x”, power users may be able to integrate this without substitution by making a guess as to the antiderivative and then making an adjustment by dividing by an appropriate constant — if this sounds confusing, just do the substitution).
Write back if you’re still stuck on this one.
Mr. Reitz
Now that we’ve simplified our expression properly, apply our function to our formula:
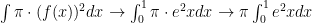
If you don’t want to use Mr. Reitz’s “handwaving” method, where you work some magic on the integral and it suddenly transforms into your answer, your problem is now set and simplfied for U-Substitution:
If anyone was confused, I hope this helps
I apologize. Those first two lines of math were supposed to appear as such:
Line 1: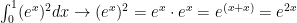
Line 2:
And to rectify one last mistake, the integrated form of the function is supposed to appear as
, instead of: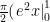 
And the final answer should appear as:
not as: 
Again, I apologize.
I’m guessing multiply e^x with e^x and integrate that.
I’m not sure that problem can be integrated.
Here’s my approach so far
1) Multiply the inside (e^x) by the exponent (2) = e^2x
2) Take antiderivative
Note: e^2x=e^2x
To integrate e^2x, you add 1 to the exponent (2x) turns to 2x^2, then you divide by the new exponent (2)
so, x^2?
since it is a indefinite integral, attach a +C for constant.
I am also currently stuck at
This is my approach:
I did substitution U=2*x dU=2dx dx=dU/2, so we get
(Pi/2)*e^u on the interval [0,1]
Final answer is: Pi/2(e-1)
Stanislav Podolski MAT 1575 -6638
This is the part that did not parse
\int_0^1 \frac{{\Pi}*e^u}{2} du
To clear that up: it’s written as such:
$ latex \int_0^1 \frac{\pi \cdot e^u}{2} du $
I can’t solve the problem 11(a) from our review sheet.
I assumed x = 6 sinθ. But what I am getting is
∫ (dθ/6(sinθ)^2 cosθ). then I am stuck.
Is there anyone who got the correct answer?
Hi, I am Gurpreet Singh
I solved the problem but it’s too o long and i’m toooo lazy so i upload a pdf. you can see it by opening this link. The quality is of pdf is poor but you can understand the concept.
https://docs.google.com/document/d/1jaTlB0eCJrpPE8JFeC5XOG7BT1VGJ_mdk_3MIRZ2i4w/edit
Thnx a lot. I got it.
OHH, and you need to know the trig identities for this problem.
u=x
a=6
a^2-u^2
u=asinθ
Yes, x=6sin (θ)
dx =6cos(θ) du
sinθ=x/6
θ=sin^-1(x/6)
I skip a few steps but,
Draw out reference triangle, substitute appropriately and simplify. You’ll wind up with
∫csc^2(u) /36 du
bring 1/36 into front = 1/36∫csc(u) du
The integral of csc^2 (u)= -cot(u)
I’ll let you work out the rest.
This question is based on the example we did in class relating to finding the area of a circle using calculus . I’m having trouble understanding why we let x=sin(θ), not cos(θ)?
Hi Melissa — in fact, it doesn’t matter: we could just as easily have used cosine instead of sine. All we really want is to be able to simplify the part under the radical using (some variation of) the identity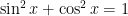
.
Mr. Reitz
oh!
For problem 9e, I keep getting the solution as 1/2. Just wondering if my calculations are wrong or the answer key is wrong?
Hi Karen,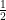
. Nice work — I’ll update the answer key on the OpenLab shortly.
You’re absolutely right, the answer is
Mr. Reitz
I just found another problem. #11b i get
Never mind. I used x^2 instead of x^3
jeffrey mongal
mon/wed 4-5:40pm
Hey Prof,
Im stuck on 9g… i can’t seem to find a u and dv that actually works or make the problem doable. Please let me know what the eaisest way is to start the problem.
Thanks!
I solved it using Integration by parts, not sure if the answer is right though), but here it is:
After substituting U=secx dV=(secx)^2 dU=secx*tanx V=tanx , and solving it I got:
(tanx*secx-ln|secx+tanx|)/2 + C
Stanislav Podolski MAT 1575 -6638
Bibin Koshy MAT 1575 -6637
I am writing this on behalf of all those individuals who are still frustrated over the topic of cylinder shells and volume of solid. I was having the same problem but I can honestly say, after following a couple of rules, i was able to solve and see the volume of solids more efficiently. I want to share this mainly towards people who are still confused about whether integrate taken in respect to y or x in the cases of both methods.
The following are rules that I followed to cope up with the frustrations and achieve the volume of a solid more efficiently.
First thing I did before tackling a certain problem is, write the rules on a sheet of paper and simply follow it afterwards :
1)
In a washer method, when you are going about x axis, you always draw a perpendicular line from the region you are going about to the region enclosed by a certain curves and that is to see what the outer region and inner region is. When you usually see x as the axis you are going about, the limits of integration and all the functions must be in x format. However, when you see vertical axis such as x=-3 or x=2, you have to take into consideration, it is a vertical axis like y axis, therefore, everything must be in y format. In addition, something like y=2 or y=-7 is a horizontal axis or looks similar to the x axis, therefore, everything must be in the dx format. Another thing that one must take it to consideration, when you are going about the y axis, you have to convert given functions such as y=X^3 and convert it into a way that x is isolated, which in this case is x=f(y)or x=3sqroot(y). The thing to remember is, when you see a problem related to washer or disks, always look at the axis the problem is telling you to go about and integrate it accordingly.
2)
The cylindrical shell method:
Compared to the first method, washer or disk method, shell method is quite different, especially when integrating. In the washer method, all we had to do was look at whether x=3 or y=2 shows a vertical or horizontal axis, and from it, we could deduce that the integration must be done accordingly to the axis. However, for the shell method, that is not the same. When you want to find the volume of a solid using the shell method that is going about the x axis, people usually think the integration must be with respect to x, but when people see the clear picture, they will see that they are wrong and that everything is taken in the format of y. Likewise, when a problem says, ” find the volume of a solid using the shell method that is going about the y axis this time, everything must be taken in respect to dx or x.
*Like the first method, when you take integration with respect to y for the washer, always make sure the function such as y=sqrootof (x) is converted into a way you get the x isolated, like in this case x=y^2, so that proper integration can be done.
By knowing these key concepts of how they are different and similar , one can tackle these kind of problems related to volume more efficiently.
That’s good observation. I followed the same rules and i get through that chapter as well.
i take back what i said in class LOL i read it i think i get it
I am having trouble grasping the trigonometric integral problems. Can someone please explain some steps for me ?
Trigonometric integral problems are like regular integral problems except this time you change the “name” of the trig function to one that is equivalent helps simplify the problem. If you already know the anti- derivatives or derivatives, it will be a little easy to integrate. When it comes to trig functions with exponents, split it to where at least one new trig identity matches one you already know then proceed with the suitable integration method.
Also, KNOW ALL TRIGONEMETRIC IDENTITIES, including degrees and equivalent fraction terms. Memorize almost everything important THEN try to tackle the problems.
The point is to change it so integration could be easier than if you would’ve left it as is. For extra help outside the classroom… here’s a link- http://www.youtube.com/watch?v=lTqnlihOC4o&feature=fvwp&NR=1
Hope that helps!
Thanks it did !
For question number 2 on the review sheet, I am not sure how you get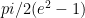
, where do I o from there?
I have
idk whats wrong with latex.. I have pi/2 integral from 0 to 1, of function e^u
Hi Keyla — I think it just didn’t like the backslash in front of the e^u.
in the first quadrant bounded by the graph of y=4ln(3-x),the horizontal line y=6 and the vertical line x=2. find the volume of the solid generated when the graph is revolved about the horizontal line y=8.
pi $latex\int_0^{\2}/ (6-4ln(3-x)^2)
ans = 168.80
means pi is in outside ,then the intergral sign which goes 0 to 2 and in the (6-4ln(3-X)^2)
i’m having the most difficult time trying to integrate
. i think i used all possibilities for my u’s, du’s, and dv’s and i still keep getting the wrong answer. can anyone help me get on the right direction?
i would also want to know is how do you know you are getting the right or wrong answer when you are using integration by parts…?
thats exactly what i got. thanks
im having a little problem with question #4
pi \int_-2{\2}\((4- x^2 +5)^2 – (x^2 -4 +5) from that i got;
(-x^2 + 9)^2 – (x^2 +1)^2 then foil;
(x^4 -18x^2 +81) – (x^4 +2x -1) after that i got this;
pi \int_-2{\2}\-20x^2 +80
for this question this is the setup after this just integrate it and the bounds of the integral you get by x^2-4=4-x^2 and you should get x=-2,2
![\int_-2^{\2} \2pi(x+5)[(4-x^2)-(x^2-4)] dx](https://s0.wp.com/latex.php?latex=%5Cint_-2%5E%7B%5C2%7D+%5C2pi%28x%2B5%29%5B%284-x%5E2%29-%28x%5E2-4%29%5D+dx&bg=ffffff&fg=000000&s=0 "\int_-2^{\2} \2pi(x+5)[(4-x^2)-(x^2-4)] dx")
Prof.Reitz am putting the formula in latex but doesnt work \int_(-2)^{\2} \2\pi(x+5)[(4-x^2)-(x^2-4)] dx
am adding latex and $ at the end but cant work it out.
Hi Ximena — two things: in the bounds of the integral, use curly brackets instead of parentheses around the -2, and later on don’t put a backslash in front of the number 2 (occurs twice). Give that a shot.
-Mr. Reitz
Hi Ximena – nice job on the latex! Be careful — this problem requires washers, not shells, since we are rotating around the horizontal line y=-5. This is going to affect your integral.
do we have to know the trigonometric substitution by heart?
Unfortunately, yes! (but just the first two columns of the table – the function, and the corresponding substitution)
Igor. M.
Heyy). In problem 8c I cant figure out how to integrate. Do I use technique of integration by parts? Where would I start ?
integration by parts twice (or three times)
keep your dv= to e^x and u=x^3 dv stays the same while u will change
Hi Prof.Reitz How should I start question 11b .
Hi Prof Reitz.
i don’t understand how to do problem 10 in the review.
For problem 10
x^2+y^2=9 and the center is (0,0)
thats the set up for the problem
the integral goes fro -3 to 3
I have a problem on how to start with problem 8C.
Should I let u = x^3? or e^x?
well for this problem you have to use integration by parts three times. the first case U will equal
the second case U will equal to 
and the 3rd case U will equal 
Because this is a rather long problem pay attention to your constants and which integral each constant is a reference to.
$latex \int x^3e^X= x^3e^x-3x^2 3xdx
=e^x(x^3-3x^2+6x-6)
well for this problem you have to use integration by parts three times. the first case U will equal
the second case U will equal to 
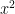and the 3rd case U will equal 
Because this is a rather long problem pay attention to your constants and which integral each constant is a reference to.
When I study a particular problem I like stop write the steps I have to follow to complete the problem as I work on it. It is sort of time consuming but it helps me to remember what I have to do to get a problem done successfully.
I do the same thing !
(even nerdier) i use a white board since my handwriting is equivalent to a five year olds, when things are bigger it helps me see them better and i can draw; clear cut lines and notes to myself
I just wanted to share a weird way that i remember the integration by parts formula; although it isn’t the most difficult formula to remember…I just say to myself before a I.B.Parts question
“You are so DeVious for wearing UV sunglasses to protect from the Negative voodu”
u dv = uv – vdu
You devious UV (negative sign) Voodu
You just have to remember to put the integral at the beginning and after the negative so u will have the proper form below:
Dig it!
Too funy…
funny*
I’m still slightly confused by the basic concept of Cos2x… I can’t seem to remember how to maneuver it $latex \intcos{2x}
Hi Joshua,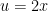
When the only thing in the way is a constant in front of x (like “2x”), try substitution:
Good luck,
Mr. Reitz
problem 9) G
$ latex \int sec x^3 dx $
i used
u= secx du=tanx secx
secx^2* secx
(tanx^2+1)*secx
secxtan^2x+ $ latex \int secx dx $
problem 9) G
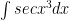
i used
u= secx du=tanx secx
secx^2* secx
(tanx^2+1)*secx
secxtan^2x+
I’m having slight difficulty with 9d. off the Review sheet: Any suggestions? please and thanks
i just finished that one take out a sec*tan so that it’s now sec^6tan^2 tan*secdx then use u=sec du= sec*tan dx 🙂 (don’t forget the trig indent for tan^2)
Thanks!
11B
$ latex\int_sqrt[2]^{2}\frac{1}{x^2sqrt[x^2-1]$
why is $latex\sqrt{2} is equal to sec Theta ?
$ latex\int_sqrt[2]^{2}\frac{1}{x^2sqrt[x^2-1]$
$latex\sqrt{2}$
-don’t work.
For question #8c:
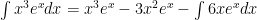
I got
I I used
I got
I used the intergration by parts again.
I got
intergration by parts again:
For problem #6, When you do u-substitution for:
$latez \int_0^1 2{\pi}x \sin({{\pi}x^2})dx$
and get:
u =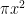
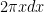
du =
I understand that you must then change bounds of the interval to
and I understand how to do it, but I don’t understand why.
Can someone explain it to me?
Fixed.
For problem #6, When you do u-substitution for:
and get:
u = {\pi}x^2
du = 2{\pi}xdx
I understand that you must then change bounds of the interval to
\int_0^{pi}
and I understand how to do it, but I don’t understand why.
Can someone explain it to me?
FINAL revision. (They should REALLY implement an “edit post” feature.)
For problem #6, When you do u-substitution for:
and get:
u =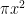
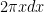
du =
I understand that you must then change bounds of the interval to
and I understand how to do it, but I don’t understand why.
Can someone explain it to me?
After doing the substitution, u is the variable of integration, not x.. so the limits have to been put in terms of u in respect to x…. or you cannot finish the problem since you changed to u’s but left the integrals with x.
I hope I kind of cleared it up a little.
(Math is hard to explain in words for me) : )
That makes sense. Thanks a lot!
I have a hard time working arbitrarily. I have to know why I’m doing something before I start doing it.
Hi, can anyone help me with question 8D from the review sheet? Using integration by parts i have u=sinx and dv=e^x but each time i finish integrating i am left with what i started with, so i am going in circles. What is the trick? What can i do?
\int_e^x sinxdx
u=e^x du=e^x dv=sinx v=-cosx
\int_e^x sinx=e^x-cosx-\int_-cosx e^x dx
\int_ e^x sinx=-e^xcosx+\int_e^x cosx dx
2\int_ e^x sinx=-e^x cosx+e^x sinx
\int_ e^x sinx=1/2 e^x(sinx-cosx)+C
I could not get the integral sign to work but that’s how I did (8)d.
you will see this eventually then just divide the two so it becomes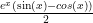
oooooh, i see it now thank you 🙂
Hi, i am having problem solving question 11c on review.
Hi, i am having problem solving question 11c on review.
Just ran into some tips that I found helpful regarding to when to use the washer or shell method.
When the dependent variable and the axis parallel to the axis of rotation are the same, use the washer method.
When the dependent variable and the axis parallel to the axis of rotation aren’t the same, use the shell method.
Hopefully this will help someone else. Good luck to everyone tomorrow!
Wow…….. it really did . Thanks a lot!
For question #8c:
I got $latex\ e^x(x^3-3 x^2-6 x-7)+C$
I I used $latex\ u=x^3$ $latex\ dv=e^x dx$
$latex\ du=3 x^2 dx$ $latex\ v=e^x$
I got $latex\ x^3 e^x-\int e^x 3 x^2 dx$
I used the intergration by parts again.
$latex\ u=3 x^2$ $latex\ dv=e^x dx$
$latex\ du=6 x dx$ $latex\ v=e^x$
I got $latex\ x^3 e^x-3 x^2 e^x-\int 6 x e^x dx$
intergration by parts again: $latex\ u=6$ $latex\ dv=e^x dx$
$latex\ du=dx$ $latex\ v=e^x$
$latex\ x^3 e^x-3 x^2 e^x-6 x e^x-6 e^x-\int e^x dx$
$latex\ e^x(x^3-3 x^2-6 x-6-1)+C$
For question #8c:
I got
$latex\ e^x(x^3-3 x^2-6 x-7)+C$
I I used
$latex\ u=x^3$
$latex\ du=3 x^2 dx$
$latex\ dv=e^x dx$
$latex\ v=e^x$
$latex\ x^3 e^x-\int e^x 3 x^2 dx$
I used the intergration by parts again.
$latex\ u=3 x^2$
$latex\ du=6 x dx$
$latex\ dv=e^x dx$
$latex\ v=e^x$
$latex\ x^3 e^x-3 x^2 e^x-\int 6 x e^x dx$
intergration by parts again:
$latex\ u=6$
$latex\ du=dx$
$latex\ dv=e^x dx$
$latex\ v=e^x$
$latex\ x^3 e^x-3 x^2 e^x-6 x e^x-6 e^x-\int e^x dx$
$latex\ e^x(x^3-3 x^2-6 x-6-1)+C$
I don’t know why it does’t work???
$latex\ e^x(x^3-3 x^2-6 x-7)+C $
I I used
$latex\ u=x^3 $
$latex\ du=3 x^2 dx $
$latex\ dv=e^x dx $
$latex\ v=e^x $
$latex\ x^3 e^x-\int e^x 3 x^2 dx $
I used the intergration by parts again.
$latex\ u=3 x^2 $
$latex\ du=6 x dx $
$latex\ dv=e^x dx $
$latex\ v=e^x $
$latex\ x^3 e^x-3 x^2 e^x-\int 6 x e^x dx $
intergration by parts again:
$latex\ u=6 $
$latex\ du=dx $
$latex\ dv=e^x dx $
$latex\ v=e^x $
$latex\ x^3 e^x-3 x^2 e^x-6 x e^x-6 e^x-\int e^x dx $
$latex\ e^x(x^3-3 x^2-6 x-6-1)+C $
Z_Z
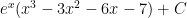
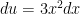
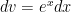
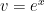
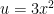
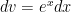
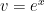
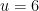
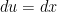
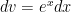
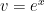
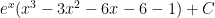
Z_z
I I used
I used the intergration by parts again.
intergration by parts again:
for the -1 i’m not sure where you got it from the last one int e^x is already factored out unless you put in du=1 but +C is there
$latex\ u=6$
$latex\ du=dx$
$latex\ dv=e^x dx$
$latex\ v=e^x$
$latex\ x^3 e^x-3 x^2 e^x-6 x e^x-6 e^x-\int$ $latex\ e^x dx$
$latex\ e^x(x^3-3 x^2-6 x-6)+C$
It should just be the above answer, no (-1) after the -6 is necessary.
Hi guys — just get rid of the slash \ after the word latex.
-Mr. Reitz
hi anyone can share the problem 9e from the review sheet?
which rule is it used?integration by parts?
I think that a good exam problem would be to find the volume of
y= 1/x , x=1, x=2, y=0 about the x-axis.
prof reitz doesn’t give easy problems like this, if a problem is not 2 pages long, then he probably wont give it in the exam ;p
I have a question on #4.
How to figure out which fuction is the small radius and the large radius?
If you’re still in the dark about that for #4, the trick to figuring out that one is pretty simple. Whichever function is further away from the line that you’re rotating around is the larger radius. So since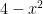
is further away from 
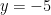, it’s the larger radius in the function. This concept works all the time.
If that’s still not quite enough for you, you can use a more mathematical method and a less visual method, but they both come out to the same thing. Plug one constant value for x into both of your functions within the region that we’re integrating. You take those values and find the distance from the line around which you’re rotating and see which comes up bigger.
For example:
To find the distance between that value in either function and the line that you’re rotating around:
For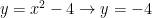
:
For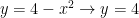
:
I was rotating around the line x=-5.
I have a question for the third question on the review sheet. We are supposed to integrate the region bounded by: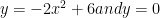
In order to find the bounds for our integral, we use a system of equations, which should look like this: 
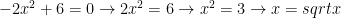If this is correct, then why are the bounds of integration [0,3] instead of ![[0,\sqrt{3}]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Csqrt%7B3%7D%5D+&bg=ffffff&fg=000000&s=0 "[0,\sqrt{3}]")
? Did I go wrong somewhere, or is the answer in the key flawed?
To clear that first part up a bit:
and 
The function is $latex\ y=-2x^2+6x$ not $latex\ y=-2x^2+6$
so $latex\ 0=-2x^2+6x
x(-2x+6)=0
x=0 -2x+6=0
x=3
Thanks very much. Not sure why I didn’t see that one.
you are welcome
so
x(-2x+6)=0
x=0 -2x+6=0
x=3
This isn’t specifically related to the homework, but I figured I’d throw it on here:
Happy Pi Day!
lol
Back at ya – have a piece of pi today 🙂
for number four i dont know what to do. there is an extra 20.. when i get ride of 20 it works but i dnt kno how i got the extra 20.
lol http://www.youtube.com/watch?feature=player_embedded&v=enhxOTVNuNM
Funny! I am extremely disturbed that I find myself nodding in agreement with many things she said…
Dear Professor, I am sorry I could not post this yesterday. I have a problem initially recognizing some problems from the onset, but I am getting better. My other problem is when I set up the equations; I am having some algebraic problems, especially sign distribution. I am trying very hard to slow myself down, as I work through the longer problems.
HI Prof, Quick Question – Are you going to provide us with the reduction formulas if need? Because we need to use the reduction formula for 9G.
It is technically possible to do 9g using only things we’ve covered (convert secants to tangents, integration by parts, and the integral of secant), BUT it’s a tricky one – I won’t put it on the exam.
In case you are having trouble remembering integration by parts here’s an awesome tutorial!! http://www.youtube.com/watch?v=dqaDSlYdRcs
I dont know how to create a new topic but i need help on a webwork question. I’m asked to find the volume of a solid between the regions y=17 and y=x+72/x. I tried the shells method and used the formula $latex\int_8^{9}(x+3)(x+\frac{72}{x}-17)dx$ I also tried washer with the formula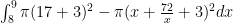
I dont know how to create a new topic but i need help on a webwork question. I’m asked to find the volume of a solid between the regions y=17 and y=x+72/x. I tried the shells method and used the formula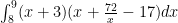
I also tried washer with the formula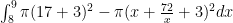 
I forgot to mention that it rotates around x= -3.
2pi should be in the first formula. That was an error.
When should I use cylindrical shells or the washer method for solving volumes of shapes.
\int \frac{ln(x)}{x^5} how is the du for this found if u = ln(x) and du=1/x^5 dx how can you get 1/x and dx alone
\int \frac{ln(x)}{x^5} how is the du for this found if u = ln(x) and du=1/x^5 dx how can you get 1/x and dx alone