UPDATE: LaTeX tester. Want to test out your LaTeX code before you post it in a comment? There is a LaTeX tester here, where you can type in your formula, hit the button, and see how it looks: http://samples.geekality.net/latex/
NOTE: When you use the test, do NOT include the dollar signs or the word “latex” — just include the stuff in between.
Assignment (due at midnight on Monday, February 20) . Create a problem that could appear on the first exam, and post it in a comment as a reply to this assignment. It should satisfy the following:
- It can be from anything we have studied so far this semester, from the first day of class up through Section 6.4, Addition and Subtraction of Radicals.
- It must be a reasonable exam problem — not too easy, not crazy hard (I will be the final judge of what counts as a “reasonable exam problem”) — and you must be able to solve it yourself. For ideas, look at the homework assignments, the group work from class, your notes, and so on (you can use these sources as inspiration, but please don’t copy problems from them directly). If you wish, you can also ask short-answer, explanatory type questions, like “Explain in your own words ….” or “Why does …” or “What’s the difference between xxx and yyy?”. Bonus points for creative questions!
- It must contain some kind of mathematical symbols, which must be posted using correct mathematical notation. How do you do this? See below.
Extra credit. Solve one of your classmates’ questions, and post the solution as a reply. Your solution MUST be posted using correct mathematical notation.
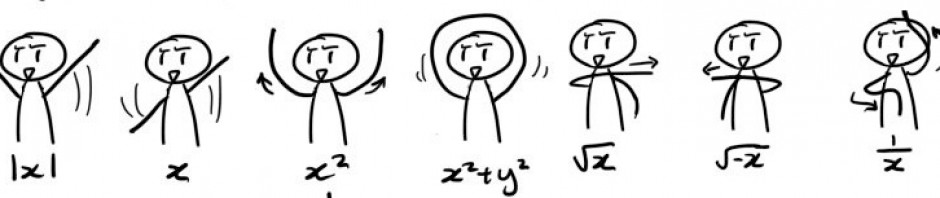
What’s the point of this assignment? Two things: First, to make you think about what kinds of problems will be on the exam — and creating a problem forces you to consider this from a different perspective (what should be on the exam?) than simply practicing problems. Second, I want you to start learning how to type mathematics on the OpenLab — how do you make exponents, square roots, and so on?
Typing math on the OpenLab. This is not hard — BUT it takes a little getting used to. Here’s an example. If you type this into a comment:
Here is a square root: $latex \sqrt{x^2+1}$
then (after you post the comment) you should see this:
Here is a square root:
Each equation or expression begins with “ created by computer/math god Donald Knuth (and used by basically all math and science professionals in the universe). In between “
, use “^” (just like in your graphing calculator).
Here are a few more examples:
| Type this: | to get this result: | |
| A. | ||
| B. | ||
| C. |
Some notes about these examples:
Example A (fractions): The code for fractions is “\frac{ }{ }”, with numerator inside the first set of curly braces { } and the denominator in the second set.
Example B (big parentheses): In many cases you can just use regular parentheses “( )”. BUT if you want your parentheses to get bigger, for example to wrap around an entire fraction, then you should use “\left(” and “\right” instead.
Example C (radicals and nth roots): Regular radical signs, like the first one, use the “\sqrt{}” command. For higher roots we use “\sqrt[n]{ }”, where n is the index of the root (in the example, n is 5).
Hints and suggestions. Don’t start with a complicated formula. Write a comment with a short bit of math in it, and post it to see what it looks like. You can always edit the comment to make changes.
Stuck? Frustrated? Doesn’t look the way you want it to look? Let me know! Send me an email or simply post a question on the OpenLab — let me know what you’ve tried so far, and what you’re trying to accomplish.
For more examples, this link is a pretty good place to start. Want even more symbols? Here you go.



$latex 5 \sqrt{3x} + 12 \sqrt{3x}
Looks good!
17
5\sqrt[3]{ab} + 2\sqrt[3]{ab}
Nice!
$\sqrt7[3]{ab}$
OKAY I GIVE UP! this is really frustrating!
one more 7\sqrt[3]{ab}
FINALLY! 🙂
Maisa1491 — nice job! Your persistence paid off in the end.
Tricky one! I like this problem, but (if it scares you) I wouldn’t put it on the exam — it’s just a little too challenging. I’ll accept it for the assignment though. Looks good!
I think I answered it wrong the correct way might be this
Okay I’m wrong. lol
Great! Nice combo of fractions and exponents.
$latex \left(\frac{x^2}{16}\right)
or maybe its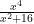
Looks good 🙂
Demetria Anderson (My bad)
Rodrigo Rojas
Hi Rodrigo — your problem looks good (the notation is nice!), but it would be quite hard to simplify. Raising the top and bottom to the power four means doing FOIL, or some variation of FOIL, three times in a row, each! You could make this a more do-able problem by getting rid of the addition/subtraction in the top and bottom, and replacing it with multiplication. Give this a shot, and post the results.
Thanks,
Mr. Reitz
Cristian Burgos
Hi Cristian — your notation looks great! But there is no way to simplify these two radicals. This would change if replaced the “pluses” with “times” underneath the radicals. Give this a shot, and post the result here.
Thanks,
Mr. Reitz
Profes reitz i tried to test mine on the other site, and its still not coming out either. I can’t get this to work
Hi Brina — you’re really close. You are just missing the letter “r” in “\sqrt” (both times). Fix this and re-post your problem!
Mr. Reitz
Prof reitz i fix it but its still not working
Hi brina — that’s frustrating! Post what you’ve got and I’ll take another look.
=62
Tony Liu
that supposed to be a minus before the 4!
wait BAD QUESTION! … how about..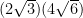
Good fix — I’ll take it!
Catherine — you’re almost there! Just add a space after the word latex, and try it again.
Mr. Reitz
ps. nice problem!
I don’t know, it just not work for me…
Try it again — if it’s wrong, I’ll point you in the right direction.
Mr. Reitz
Good!
Creative – I like it.
there needs to be a space before the -4 and the latex
Thanks a lot! 🙂
great!
$latex\sqrt[4]{3}+7\sqrt[4]{3}-\sqrt[4]{14}
Jesse Mohammed
Hi Jesse — I like it, but there is no way to simplify these radicals. The real problem is the addition underneath the radical sign — get rid of the “+ 2” in each radical, and you’ll be good.
$latex \sqrt[4]{3}+7 \sqrt[4]{3}- \sqrt[4]{14}
$latex \sqrt[4]{3} + 7\sqrt[4]{3} – \sqrt[4]{14}
minyi yu
Nice job!
Ok so i tried couple of them but for some reason i cant seem to get it to work..my problem was.. (3/8m)/(7m^2/2)..
out of that the only part i got was
but the rest i could not get. :/
couldnt get get the second half.
imfh450 — this is a tricky one! You’ll need to use three different “\frac”s. Here’s a similar example showing
\frac{ \frac{1}{2} }{ \frac{4}{3} }
The first \frac is for the big fraction, the second is the top, and the third is the bottom. See if you can use this as a model.
Simplify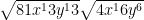
sorry the last one seem challenging so here is a simple one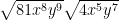
Looks good !
\sqrt{x^9+46} -\frac{x^2+7x}{10+5x}
heyyy its not working 🙁

i got it 😀 ^^
Nice job!
-Talia Ordonez
Looks good, but I’m not sure what to do — I can’t figure out how to simplify it! Can you explain, or make a change?
^^^^-Todd Manning
Nice notation, but neither of these radicals can be simplified, mainly because of the addition underneath the radical signs. If you change these to multiplication instead, it would be fine.
Mr. Reitz
Hi Tatiana,
You’re close! The backslash always comes just before the word sqrt, so (for example) you might have: 4xy\sqrt{x}, but you wouldn’t have \4xysqrt{x}. Make this change and I think it’ll work.
Regards,
Mr. Reitz
Hi cdavis — the problem looks good (although there isn’t that much simplification we can do — only the a’s).
Looks nice, BUT neither of these radicals can be simplified, mainly because of the addition underneath the radical signs. If you change these to multiplication instead, it would be fine.
Notation looks good! Unfortunately, neither of these radicals can be simplified, mainly because of the addition underneath the radical signs. If you change these to multiplication instead, it would be fine.
Sorry im late, but decided to try it anyway….
dont know where to find the opposite looking / , any help
The answer is 146!
Ok all this latex is irritating! lol i’m testing out the equation given as an example!
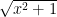
Okkkkk this a little bit of a pain in the ass, I’ll bring this issue up in class on Tuesday! >:-(
But for now here’s my equation:
Hi meyvin72 — you’re on the right track (and yes, latex can be a pain in the *ss). Here are my suggestions:
put a space after the word latex. you don’t need a backslash before the parentheses (. In between the the parentheses, for a nice “multiplication” dot, instead of using a period use \cdot (this is a “center dot”). Try these updates and see how if it works!
Mr. Reitz
Pingback: The Open Road
Pingback: This Week in OpenLab! May 7th Edition | The Open Road
Pingback: OpenLab #3: Flipping the class – Inverse Laplace Transforms and Partial Fraction Decomposition | MAT 2680 Differential Equations