MAT1275 College Algebra and Trigonometry, Spring 2017

I am posting the remaining problems from the Final Exam Review, and there are also problems from the Proving Trigonometric Identities worksheet over on Piazza.

UPDATE: I have posted the remaining problems from the Proving Trigonometric Identities worksheet over on Piazza. You may submit a student solution for a homework point to any one of these (if it has not already got a student solution). Please follow these instructions: Either type in your solution using good Math notation as described in this post, or else write up your work NEATLY and take a CLEAR and LEGIBLE photo and post it as the student solution. Illegible solutions or solutions which do not use the method in the worksheet will be deleted and receive no credit. (You should put a bit of effort into this!)

——————————————————

(after Test 4)

Topics:

• Logarithms and exponents
• Finding exact values of logarithms
• Properties of logarithms

Here are the resources that I use in class:

Definition of logarithms (Math is Fun) – this goes all the way back to the very basics.

Introduction to logarithms (Math is Fun)

For next time: Working with exponents and logarithms (Math is Fun)  – you only read down to where it says “The Natural Logarithm and Natural Exponential Function”

Those sources from Math is Fun contain just about everything you need to know about logarithms and using them, so far!

My slideshow about logarithms: (I’m still working on this and I may upload a more extensive version, so check back!)

MAT1275-LogarithmBasics-slideshow

The Precalculus textbook (we use some examples from here, Session 13, Example 13.9 on p. 191.)

Homework:

• Right about now would be a good time to review my Course Policies especially as they relate to grading.
• Review the examples discussed in class. Make use of the resources linked above: they are focused on exactly what we need to work on!
• Do the following problems: (They are from the Precalculus textbook linked above: you can check your answers by looking into the answer sections there)
  Precalculus-Tradler-Carley-ExercisesLogs
• Also find the exact value of these without using a calculator:
  1. 
  2. 
• Do the WeBWorK: due by Sunday 11 PM, but start early and try to do distributed practice!

NOTE: You may put any of the above homework problems on the board at the start of class next time. Please do NOT put the Final Exam Review problems on the board until I call for them! We will have to do one more very short topic before that, which is solving simple exponential equations using logarithms. It will be helpful if you read ahead:

For next time: logarithm practice worksheet: basic skills 8 logarithms

Here is the updated Final Exam Review sheet (the one on the Math Department website has NOT been updated): we will have to provide solutions to problem 10 in our method.

1275_Review-Sheet-2017

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

(Copied from a post on the Piazza discussion board)

How to type in math formatting in Piazza:

This is the easiest way to do it: do this if at all possible! Using a phone should be a last resort.

If you are on a computer or logged into Piazza in a browser window, you should see a button in the toolbar of the editing window that says f_x

If you hover your cursor over that button, it says “LaTeX Equation Editor”. Click on that button to get a collection of drop-down visual menus that show you various choices of formatting, Greek letters, symbols, and so on. When using this editor, it is best to enter your entire mathematical expression or equation in the editor all at once, rather than going back and forth. So as soon as you want to start typing in a mathematical expression, click on that button and work in the editor window until the expression is complete.

If you are working in the handheld app, you will not be able to use this visual editor. You can still use math formatting as follows:

Your math expression should be enclosed in double dollar signs: put $ $ at the beginning and end of the expression or equation. (But no space in between the dollar signs.)

To enter a square root (radical) sign, type \sqrt{} with the radicand inside the braces.

For example, \sqrt{3} will give you nicely formatted.

To enter a fraction (rational expression), type \frac{}{} with the numerator in the first set of braces and the denominator in the second set of braces.

For example, \frac{2}{3} will give you .

To enter “plus or minus”, type \pm

Example: The quadratic formula would be typed in as

x = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a} enclosed in double dollar signs to give you

To enter , type \pi

To enter the degree mark, type ^{\circ}

So 47^{\circ} gives

To enter a trig function (and make it look nice), you can enter \sin{}, \cos{}, \tan{}, etc.

So \sin{x} gives you a nicely formatted 

To make parentheses that are the right size, you can enter them as \left( and \right) – you don’t need to do this, but it makes the expression look nicer.

Here is an example:

with regular parentheses: \sin(x – \frac{\pi}{2}) gives

using \left( and \right): \sin\left(x – \frac{\pi}{2}\right) gives

Don’t forget to enclose the entire expression or equation in double dollar signs!

#pin

This is one of the problems which are given in the Test 4 review. Please do not try to just memorize the words I have used here. Make sure that you understand what you are doing at each stage and that you can say it clearly (and using correct vocabulary when it is called for).

Solve the equation for in the first cycle, as we did in the Application in class: show all work, including use of the unit circle, and explain in words what you are doing at each step.

I will first substitute in place of the input $\latex 40\pi t$ to simplify the equation:

Next I solve this equation for :

or 

I solve this equation for all the solutions in :

Since the sine is the second coordinate,  find points on the unit circle whose second coordinate is 0. There are two points: and , shown on my unit circle.

For the point , the angle is .

For the point , the angle is  .

So I have two solutions, or .

I will now find the values of by substituting back :

In the first solution,  so . (Zero product property.)

In the second solution, 

So there are two solutions in the first cycle:   or .

Test 4 is scheduled for the first 50 minutes of class on Thursday 17 May.

The self-tests are here: These are updated and slightly corrected as of 6 PM Friday, so please make sure that you are using this new version! A couple of the problems have changed.

MAT1275Test4ReviewSpring2017

Here are copies of the unit circle for you to print out and use:

MAT1275UnitCircleBlanksCopiesNoLines

The answers are here, with descriptions of the solution methods:

MAT1275Test4ReviewAnswersSpring2017

A worked example of the applications problem is here. This shows an example of what has to be done (as we did in the worksheets) and how it can be described in words.

Topics:

• Using the Law of Cosines to find an angle in the SSS situation (Example 3, section 7.2)

• Trigonometric Identities  (active learning worksheets)

You can see the handout online here:

trig-identities

We worked through all of part (1), and part (2)a-c, and part (3)a

At home you should complete (2) and (3), but please do not do the rest of the worksheet. We will be working on it together in class again on Monday.

Homework:

• Review using the Law of Cosines to find an angle. There is also an example of this in the Math is Fun webpage on the Law of Cosines. Or, you can view the Khan Academy video. or Patrick’s Just Math Tutorials.

• From section 7.2 in the Trig textbook, do #21-29 odd

• Complete parts (2) and (3) from the Trigonometric Identities worksheet. Do not go any further in the worksheet yet. This means that you should have completed up to the end of page 5 in that worksheet. You will work on the remaining pages together with your partner on Monday.

• Do the WeBWorK: due by 11 PM Sunday, start early! on the Law of Cosines.

• Don’t forget that Test 4 is scheduled for Wednesday 17 May. The review self-tests will be posted separately as soon as they are ready.

You may also want to take a look at the Math Department’s Final Exam review sheet. You will be able to sign up in class for a problem to present on the last class meeting day before the Final Exam.

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

Topics:

• Applications of trig equations to AC circuits (Handout)

MAT1275SolvingTrigEquationsApplications

We worked in class on the first two examples. Please complete the other two at home and bring them in next time. I will be collecting these (all four exercises). You will get 2 Homework points when you hand them in on Wednesday.

• Solving triangles which are not right triangles: (Sections 7.1 and 7.2 in the Trig book)

The Law of Sines

The Law of Cosines

Notice that in order to use the Law of Sines, you need to know at least one angle and its opposite side. We used it in the ASA situation (Example 1 Section 7.1) and also in Example 2 of Section 7.2 to find an angle.

The Law of Cosines can be used if you know two sides and their included angle (the SAS situation), to find the other side. See Example 2 in Section 7.2.

Next time we will see how to use the Law of Cosines to find an angle in the SSS situation.

Homework:

• Review the two application examples we worked in class and finish examples 3 and 4 on the handout. Bring both pages to class to hand in next time.

• Review the examples we worked in class using the Law of Sines and the Law of Cosines.

• Do the assigned problems from sections 7.1 (all of them) and 7.2 (up to #11 only) in the  Course Outline

• Do the WeBWorK: the first part is due by 11 PM Tuesday, start early! The Law of Cosines assignment is not due until later because we have not yet finished discussing its use.

You may also want to take a look at the Math Department’s Final Exam review sheet

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

This post is delayed while I get some files in order for you. In the meantime, review what we worked on in class, and you cans start the WeBWorK (only 2 problems!) and this:

Find all exact solutions in for each equation, using the unit circle:

1. 
2. [Hint: first isolate the to get a basic trig equation.]
3. 
4. 
5. 
6. 
7. 

Topics:

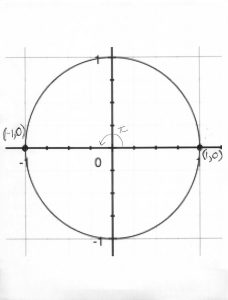
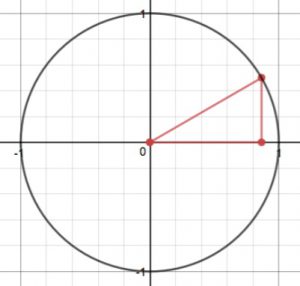
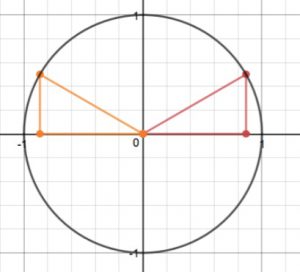
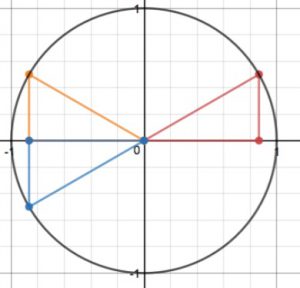
• Reflecting the special right triangles into the four quadrants to get other important points on the unit circle

• Angles (rotations) which terminate on an axis and the points on the unit circle

• Now that we have all of these important points, put them in the big unit circle picture I handed out. You can download another copy of it and use it for practice:

UnitCircleToFillIn

• Finding values of the trig function using the unit circle and reference angles.

We did this for two angles, one positive and one negative. (Sorry, I don’t recall which angles they were: if you know, please leave a comment!) The important thing is first to draw the angle, and then find its reference angle. We can then use either the unit circle or just the special right triangles to find the value of the trig function we want.

To draw angles which are given in radians without translating into degrees, I do as follows:

For example, if I want to draw the angle , I first rewrite it as a mixed-number angle:

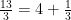
So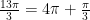 

I remember that 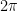wraps one time around the circle, so 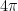will wrap twice around the circle, and then I go another 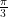which is one-third of a straight-line angle (since 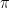is a straight-line angle). This ends up in the first quadrant and I can easily see that my reference angle is  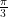by drawing it this way.

It may seem really indirect to think this way, but the opposite is true: you are tying your mind to the appearance and actual size of the angles and associating them directly with the radian measures, so in even the short run it will benefit you greatly to do this rather than translating into degrees! Radians are actually much easier to work with than degrees once you get used to them.

• Finding angles if we know the value of the trig function – we will return to this next time!

Our example: what is the angle between 0 and 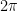if ? We saw from the unit circle picture that there are two of them: one is 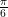, and the other is $\latex \frac{5\pi}{6}$. We will return to this next time! Remember that in the unit circle picture, the cosine is the first coordinate and the sine is the second coordinate.

• Inverse trig functions and solving right triangles

The inverse trig functions are defined as follows:

The inverse sine function is 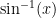:= the angle (rotation) between 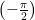and  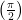inclusive, whose sine is x.

The inverse cosine function is := the angle (rotation) between and 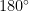 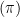inclusive, whose cosine is x.

The inverse tangent function is 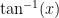:= the angle (rotation) between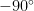 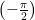and  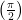, whose tangent is x.

These three functions are sometimes also called arcsine, arc-cosine, and arctangent. That means that we are looking for an arc on the unit circle, namely, a rotation. Radian measure is measuring this arc (thinking of it as a rotation on the unit circle) as we already saw looking at the discussion in Math is Fun. (here’s more)

In all three cases notice that the inverse functions give us the value of an angle (or rotation) if we already know the value of one of its trig functions. (However, it might not be the angle we want, because it picks out one of the infinite number of coterminal angles that all have that same value for the trig function. We will have to deal with this later.)

It is a good idea to read (and think of) 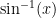as “the angle whose sine is x” and so forth. This makes you concentrate on the fact that you are looking for an angle.

There is a very nice introduction to the inverse trig functions in Math is Fun, which I highly recommend that you read!

We did part of the WeBWorK in class. You will complete it for homework. For these problems, you are using your calculator to find values for the inverse trig functions, but think about what you are doing! Later on we will be finding the values without using a calculator, using our knowledge of the unit circle picture.

Homework:

• Review what we discussed in class, and read the Math is Fun links above about radians and about the inverse trig functions.

• Fill in your unit circle. Start practicing filling it in without looking at your notes: you will need to be able to come up with these numbers quickly. Here are two videos from Patrick’s Just Math Tutorials that give a nice trick to recall the important points on the unit circle:

A trick to remember values on the unit circle

How to remember all the important points in the unit circle

HOWEVER, I have a comment and a warning about these. First of all, this is not how I remember these values: I just use the two special triangles and reflect them the way we did in class, and also the four points on the unit circle where the axes intersect are easy to see. So it is possible to remember these values without “tricks”. Most importantly (this is the warning), make sure that you understand how we got these points in the first place, no matter how you end up remembering them! The reflections and the two special triangles ae important in their own ways, and you need to have a good understanding of what we are doing before you can build on it: just memorizing things without understanding will make your life very hard indeed.

• Do the WeBWorK: there are are now three assignments (two are from before) which are due Tuesday 11 PM, don’t wait!

• Do the following problems as well:

1. Using the unit circle picture (or the special right triangles directly) but without using a calculator, find the exact values of the following: Remember first to draw the angle (without translating to degrees!)
   1. 
   2. 
   3. 
2. Using the unit circle picture (or the special right triangles directly) but without using a calculator, find the exact values of the following:
   1. The angles between 0 and 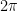whose cosine is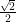
   2. The angles between 0 and 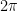whose sine is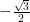
   3. The angles between 0 and 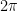whose sine is $0$

(After Test 3)

Please make sure that you check the posts for the last two classes, which contain links and notes and also homework you should do if you have not already done it! There is WeBWorK as well.

Wednesday 19 April class

Thursday 20 April class

Topics for today: (hopefully to be updated with better and more pictures)

• The two special triangles in the version where the hypotenuse is 1, and the angles are in radians. (We will try to think only in radians for the time being.) Here is a picture from another blog, but the angles are in degrees in it, alas.

The main thing when thinking in radians is not to keep translating into degrees (even in your head), but think about what the radian measure angles look like. One full rotation around the circle is ; half of that, a straight-line angle, is ; half of the straight-line angle is a right angle, which is .

To get the other important angles:

We can take half of a right angle, which will be . This is the acute angle in the isosceles right triangle, because the two acute angles in a right triangle must add up to a right angle. (All 3 angles must add up to a straight line: theorem of geometry!)

We can take a third of a straight line angle, and that will be the angle of the equilateral triangle, which is (Again, all three angles must add up to a straight line.) When we cut the equilateral triangle in half to make a right triangle, the smallest angle must be half of , namely it must be .

Visualize these angles as you go through this and think about their sizes relative to each other: don’t think of degrees at all! The relative sizes are really very important also and associating them with the radian measure will help you become very fluent in radian language.

• Embedding the special triangles in the unit circle picture and reflecting them around into the four quadrants: what’s my angle?

In class I did this for the half-equilateral triangle and its smallest angle . I will post the pictures I have of the process here, but they are not labeled with numbers yet.

Embedding the triangle in standard position (the vertex of the angle is at the origin, the adjacent side runs along the positive x-axis, and the hypotenuse extends into QI) we get this picture:

The coordinates of the vertex which lies on the unit circle were seen to be by looking at the lengths of the sides of the triangle.

Next we reflect this across the vertical axis, and we get this picture:

In the orange triangle (which is in QII), the coordinates of the vertex which is on the unit circle are  (The first coordinate is negative because we are in QII, but otherwise these are clearly the same as they were for the first triangle.)

Now we play “what’s my angle?”. What is the standard position angle (rotation) that goes from the positive x-axis to the line segment containing this point? We can see from the picture that the angle inside the orange triangle whose vertex is at the origin is the same as it was in the first (red) triangle, namely, . This angle is called the reference angle for the standard position angle we are looking for, and the orange triangle is its reference triangle.

The angle we are looking for forms a straight-line angle () when put together with that reference angle of , so our angle must be . (If you take one pie and remove a sixth of the pie, how much pie is left? Same thing for ).

So the standard position angle is  and the coordinates of the point on the unit circle are .

Now we reflect the orange triangle over the horizontal axis to get a triangle in QIII. The picture now looks like this:

The coordinates of the point on the unit circle for that blue triangle are  because in QIII both coordinates are negative.

Now play “what’s my angle?”: the standard position angle here is composed of a rotation of plus the reference angle in the blue triangle, which is again of course. So our angle is .

Finally we reflect the red triangle over the horizontal axis to get a triangle in QIV. The picture now looks like this:

The coordinates of the point on the unit circle are  because in QIV the second coordinate is negative.

Now play “what’s my angle?” one more time: The angle we are looking for forms a complete rotation () when we put it together with the reference angle in the green triangle, so the angle we are looking for is .

Finally we record the angles and the coordinates of those point into our big unit circle picture (which is eventually going to contain all of the important points on the unit circle).

Students worked with their partners on doing the same thing with the isosceles right triangles. You should finish that at home and bring it next time, and we will work on the rest of the important points then.

Please make sure that you check the posts for the last two classes, which contain links and notes and also homework you should do if you have not already done it! There is WeBWorK as well.

Wednesday 19 April class

Thursday 20 April class