The Classical Triangle Centers – centroid, circumcenter, and orthocenter.

Recall

Median-a line that joins the vertex of a triangle to the midpoint of the opposite side.

Midpoint- the point of a line segment that divides the line into two equal parts.

Perpendicular bisector- a line is cutting another line into two congruent parts and cutting at a ninety-degree angle.

Altitude- a line that goes through the vertex of a triangle perpendicular to the opposite side.

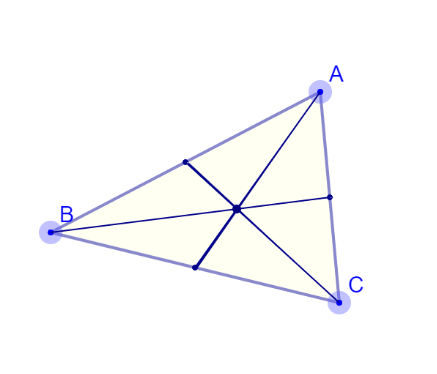
The centroid
Draw a line (called a “median”) from each corner to the midpoint of the opposite side.
Where all three medians intersect is the centroid, which is also the “center of mass”

The centroid is the intersection of the three medians. It divides each
median in the ratio 2: 1.

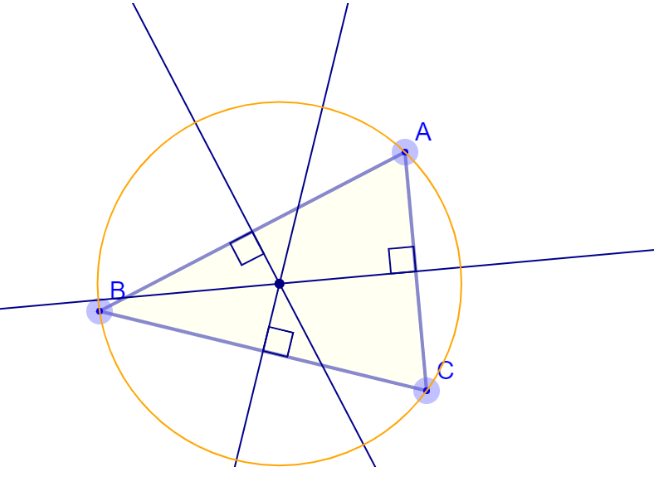
Circumcenter

Draw a line (called a “perpendicular bisector”) at right angles to the midpoint of each side.

Where all three perpendicular bisectors intersect is the center of a triangle’s “circumcircle”, called the “circumcenter”

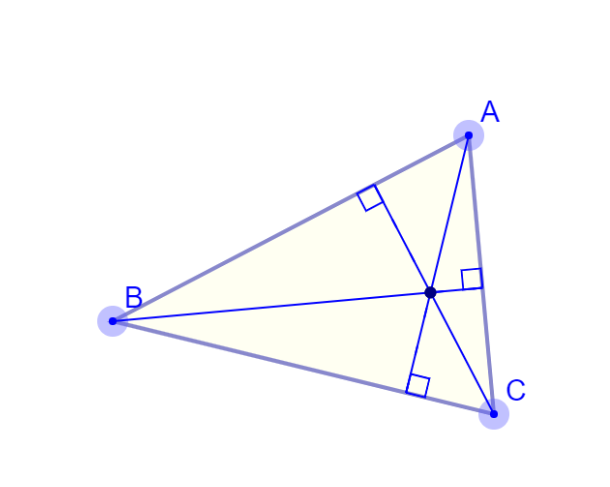
Orthocenter

Draw a line segment (called the “altitude”) at right angles to a side that goes to the opposite corner.

Where all three altitudes intersect is the “orthocenter”

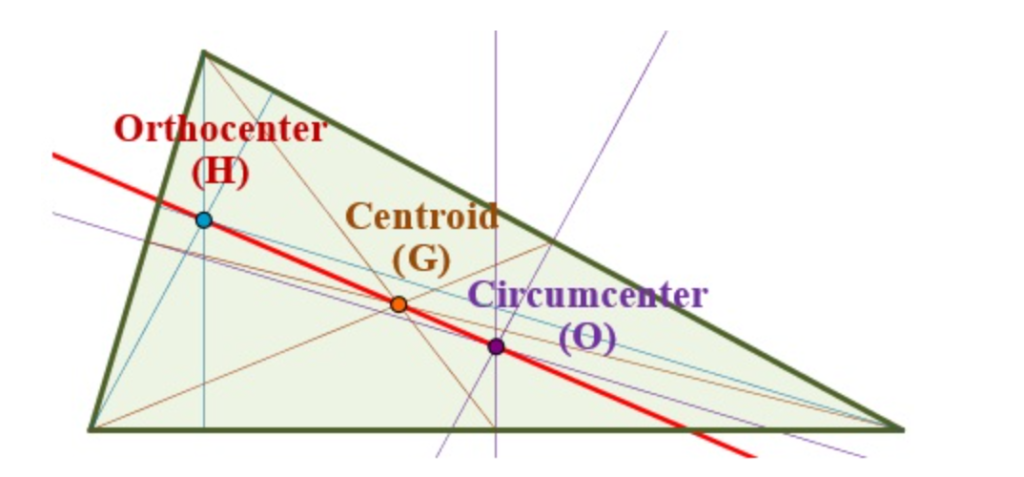
The Euler line

The Euler line of a triangle is a line going through several important triangle centers, including the orthocenter, circumcenter, and centroid.

Here is the application

https://drive.google.com/file/d/1paqcuDehGJ7Ih9gVnrhLuSXRuOJmI_fC/view?usp=sharing

Idea coming from

https://hutchinsonmodern.com/art-fairs/4/works/artworks-60-freddy-rodriguez-y-me-quede-sin-nombre-1974/

More information

https://www.geogebra.org/calculator/autxpskj

https://www.geogebra.org/calculator/kqx9k625

HW

V 2.1 to 2.5

Page 24, Q 2.2.1, 2.2.2

Page 25, Q 2.2.3

Page 26, 2.3.2, 2.3.3, 2.3.4

Page 27, 2.4.1, 2.4.2, 2.4.3, 2.5.1