Take-home test due in class on Monday, October 31

Instructions
- Answer 5 of the following 10 questions. Label each question clearly by its number.
- Provide justification to support every claim. You may use (without proving them) theorems that were stated in class and results that you proved in Homeworks 1 to 3. Reference these results clearly.
- You may use your course notes, the course OpenLab site, and official course textbooks. You may not use other resources.
- You must work independently; no collaboration allowed. The work you hand in must be your own. You may review the college, department, and class academic integrity policies here. If your work suggests outside help, you will need to meet one-on-one with your instructor.
- Write the problem down for each question. Draw and label diagrams clearly; make sure they are large and neat. See rubric and tips here.
- None of the diagrams below are to scale; they are generic representations of the figures.
- Let me know if you have any questions.
- Write at least one rough copy and a good, final copy.
- Hand in the final copy of your written work in class on Monday, October 31.
Questions
- Consider a triangle $\triangle ABC$. Let $D$ be the midpoint of $\overline{BC}$ and let $\ell$ be a line parallel to $\overline{BC}$ that intersects $\overline{AB}$ at a point $E$ and intersects $\overline{AC}$ at a point $F$. Prove that $\overline{AD}$ bisects $\overline{EF}$.
- Consider a convex quadrilateral $\square ABCD$. Let $E$ be the midpoint of $\overline{AB}$, let $F$ be the midpoint of $\overline{BC}$, let $G$ be the midpoint of $\overline{CD}$, and $H$ be the midpoint of $\overline{DA}$. Prove that $\square EFGH$ is a parallelogram. (Hint: draw a diagonal.)
- Let $\overline{AB}$ and $\overline{AC}$ be two tangent lines from a point $A$ outside a circle. Prove that $\overline{AB}$ is congruent to $\overline{AC}$.
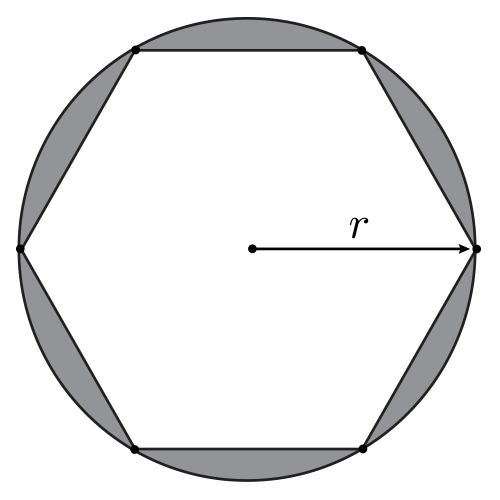
- A regular hexagon is inscribed in a circle of radius $r$ as in the figure. Determine the area of the shaded region as a function of $r$.
- Prove that the two diagonals of a kite are perpendicular to one another.
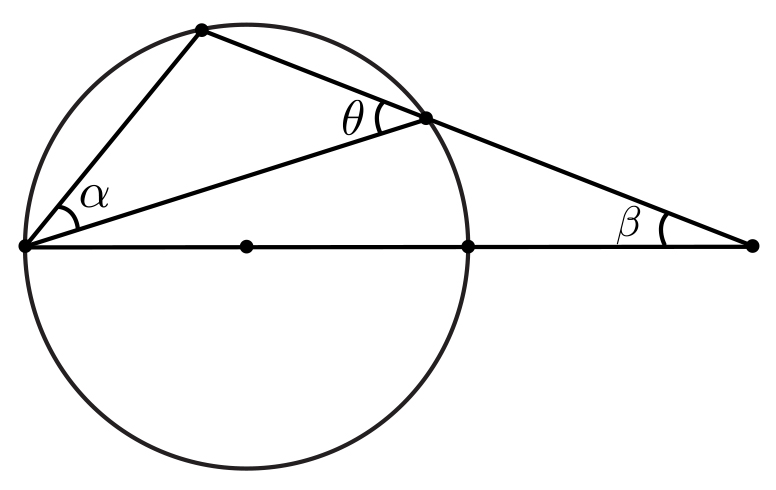
- In a circle, a chord and a diameter are extended outside of the circle to meet at point as in the figure. Determine the measure of angle $\theta$ as a function of the angles $\alpha$ and $\beta$.
- Consider an isosceles trapezoid with angles labelled as in the figure. Determine which of the following claims must always be true and which need not be true. If a claim is true, prove it; if a claim need not true, provide a counterexample or explain in words why it need not be true.
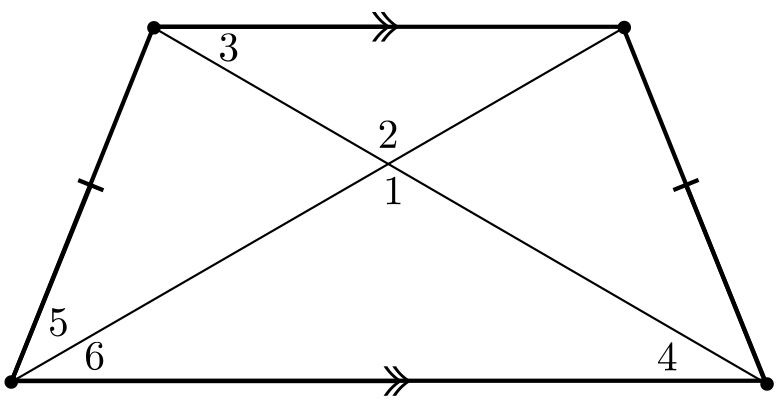
- $\angle 1 \cong \angle 2$
- $\angle 3 \cong \angle 4$
- $\angle 5 \cong \angle 6$
- $\angle 4 \cong \angle 6$
- Consider two parallel lines and a transverse line with angles labelled as in the figure. Determine which of the following claims must always be true and which need not be true. If a claim is true, prove it; if a claim need not true, provide a counterexample or explain in words why it need not be true.
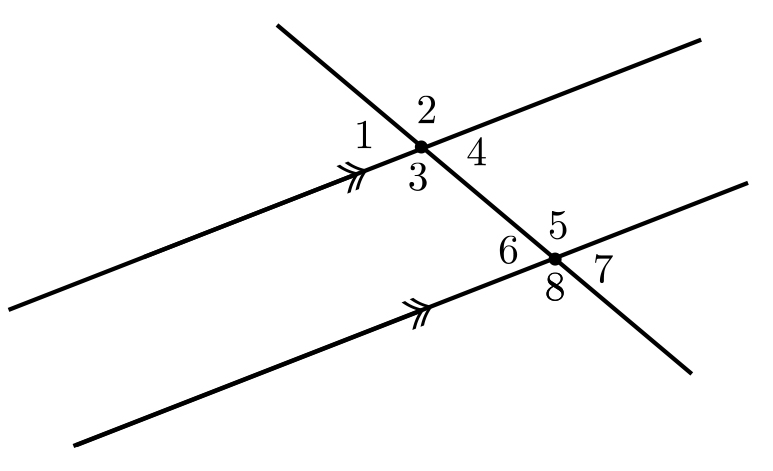
- $\angle 2 \cong \angle 5$
- $\angle 3 \cong \angle 6$
- $\mu (\angle 4) + \mu (\angle 5) = 180^{\circ}$
- $\mu (\angle 7) + \mu (\angle 3) = 180^{\circ}$
- $\angle 1 \cong \angle 4$
- Consider two intersecting chords in a circle. The intersection point cuts one chord into two pieces: one of length $a$ and one of length $b$. The intersection point cuts the other chord into two pieces: one of length $c$ and one of length $d$. Prove that $ab = cd$.
- Hint: rewrite this equation so both sides are fractions.
- Consider a circle with a chord and a line tangent to the circle at one of the chord endpoints. Let $\theta$ be the (smaller) angle between the chord and the tangent. Let $\phi$ be the central angle formed by the two endpoints of the chord. Prove that $\phi = 2 \theta$.



Leave a Reply