Give a big-O estimate for the number of operations (where an operation is an addition or a multiplication) used in this segment of an algorithm:
for 
Explain your answer.
Here there is one loop. In this loop, there are 
For each value of 
Therefore, the total number of operations is 
Most of my comments for #7 work for #8 too.
One difference is counting the number of rounds in the loop (or instances of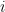
). In this case, 
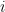goes from 
to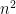 
. You don’t know what 
is so your number of rounds will depend on 
. You might be tempted to say that there are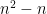 
rounds, but you can check that for low values of 
, this isn’t quite correct. If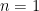 
then there should be one round in the loop, but 
. If 
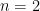then there should be a round for 
; that is, there should be three rounds, but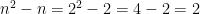 
. You can see the same pattern for higher values of 
. You’ll always need to add one to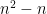 
.