Section 3.3 = #3
Give a big-θ estimate for the number of operations of this algorithm:
m := 0
for i := 1 to n
for j := i +1 to n
m := max(aiaj, m)
The values of i and j:
i := 1 <= n → n (rounds)
j := i + 1 <= n → n – 1 (rounds)
i := n + 1 <= n → 1 (Ends loop)
j := n + 1 <= n → 1 (Ends loop)
n(n – 1) + 1 + 1 = n^2 – n + 2
Exactly n^2 – n + 2 comparisons are used whenever this algorithm is applied. Hence, the algorithm has time complexity θ(n^2).




Hi Brian. There’s an error in your calculation of the number of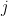 loops. Notice that
loops. Notice that 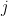 goes from
goes from 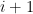 to
to  , not from
, not from 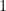 to
to  . Therefore, for different values of
. Therefore, for different values of 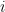 there are different numbers of possible values of
there are different numbers of possible values of 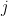 . For example, if
. For example, if  then
then 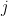 can be
can be  , so there are
, so there are 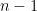 values of
values of 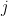 . But if
. But if 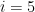 then
then 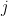 can be
can be 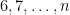 , there are only
, there are only  values of
values of 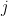 . In particular, the
. In particular, the 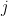 loops are getting shorter as
loops are getting shorter as 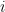 gets higher. It might be easier to check the number of values of
gets higher. It might be easier to check the number of values of 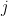 for each individual value of
for each individual value of 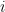 , and then add them all up. Hint: your complexity is correct but your exact number of comparisons isn’t.
, and then add them all up. Hint: your complexity is correct but your exact number of comparisons isn’t.